
【题目】已知函数![]() ,则满足
,则满足![]() 恒成立的
恒成立的![]() 的取值个数为( )
的取值个数为( )
A. 0B. 1C. 2D. 3
【答案】B
【解析】
由f(x)=(ex﹣a)(x+a2)≥0,对a分类讨论,可知a≤0时不合题意,当a>0时, f(x)的两个因式同正同负,则需在同一x处等0,则转化为﹣a2=lna的根的个数求解.
解:f(x)=(ex﹣a)(x+a2)≥0,
当a=0时,f(x)=(ex﹣a)(x+a2)≥0化为exx≥0,则x≥0,与x∈R矛盾;
当a<0时,ex﹣a>0,则x+a2≥0,得x≥﹣a2,与x∈R矛盾;
当a>0时,令f(x)=0,得x=lna或x=﹣a2,要使f(x)≥0恒成立,
则﹣a2=lna,作出函数g(a)=﹣a2与h(a)=lna的图象如图:

由图可知,a的取值个数为1个.
故选:B.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】为了选拔学生参加全市中学生物理竞赛,学校先从高三年级选取60名同学进行竞赛预选赛,将参加预选赛的学生成绩(单位:分)按范围![]() ,
,![]() ,
,![]() ,
,![]() 分组,得到的频率分布直方图如图:
分组,得到的频率分布直方图如图:
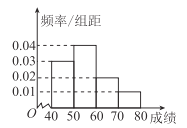
(1)计算这次预选赛的平均成绩(同一组中的数据用该组区间的中点值作代表);
(2)若对得分在前![]() 的学生进行校内奖励,估计获奖分数线;
的学生进行校内奖励,估计获奖分数线;
(3)若这60名学生中男女生比例为![]() ,成绩不低于60分评估为“成绩良好”,否则评估为“成绩一般”,试完成下面
,成绩不低于60分评估为“成绩良好”,否则评估为“成绩一般”,试完成下面![]() 列联表,是否有
列联表,是否有![]() 的把握认为“成绩良好”与“性别”有关?
的把握认为“成绩良好”与“性别”有关?
成绩良好 | 成绩一般 | 合计 | |
男生 | |||
女生 | |||
合计 |
附:![]() ,
,![]()
临界值表:
| 0.10 | 0.05 | 0.010 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() =1(a>0,b>0)的左、右焦点分别为F1,F2,点O为双曲线的中心,点P在双曲线右支上,△PF1F2内切圆的圆心为Q,圆Q与x轴相切于点A,过F2作直线PQ的垂线,垂足为B,则下列结论成立的是( )
=1(a>0,b>0)的左、右焦点分别为F1,F2,点O为双曲线的中心,点P在双曲线右支上,△PF1F2内切圆的圆心为Q,圆Q与x轴相切于点A,过F2作直线PQ的垂线,垂足为B,则下列结论成立的是( )
A. |OA|>|OB|B. |OA|<|OB|
C. |OA|=|OB|D. |OA|与|OB|大小关系不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着电子阅读的普及,传统纸质媒体遭受到了强烈的冲击.某杂志社近9年来的纸质广告收入如表所示:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
时间代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
广告收入y(千万元) | 2 | 2.2 | 2.5 | 2.8 | 3 | 2.5 | 2.3 | 2 | 1.8 |
根据这9年的数据,对t和y作线性相关性检验,求得样本相关系数的绝对值为0.243;根据后5年的数据,对t和y作线性相关性检验,求得样本相关系数的绝对值为0.984.
(Ⅰ)如果要用线性回归方程预测该杂志社2019年的纸质广告收入,现在有两个方案,
方案一:选取这9年数据进行预测;方案二:选取后5年数据进行预测.
从实际生活背景以及线性相关性检验的角度分析,你觉得哪个方案更合适?
附:
相关性检验的临界值表:
n-2 | 小概率 | |
0.05 | 0.01 | |
3 | 0.878 | 0.959 |
7 | 0.666 | 0.798 |
(Ⅱ)某购物网站同时销售某本畅销书籍的纸质版本和电子书,某班级有五名同学在该网站购买了这本书,其中三人只购买了电子书,另两人只购买了纸质书,从这五人中任取两人,求两人都购买了电子书的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列几个命题:①若![]() ,则
,则![]() ;②“若
;②“若![]() ,则
,则![]() 互为相反数”的否命题“;③“若
互为相反数”的否命题“;③“若![]() 则
则![]() ”的逆命题;④“若
”的逆命题;④“若![]() ,则
,则![]() 互为倒数”的逆否命题. 其中真命题的序号__________.
互为倒数”的逆否命题. 其中真命题的序号__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知无穷数列![]() 的各项都不为零,其前n项和为
的各项都不为零,其前n项和为![]() ,且满足
,且满足![]() ,数列
,数列![]() 满足
满足![]() ,其中t为正整数.
,其中t为正整数.
![]() 求
求![]() ;
;
![]() 若不等式
若不等式![]() 对任意
对任意![]() 都成立,求首项
都成立,求首项![]() 的取值范围;
的取值范围;
![]() 若首项
若首项![]() 是正整数,则数列
是正整数,则数列![]() 中的任意一项是否总可以表示为数列
中的任意一项是否总可以表示为数列![]() 中的其他两项之积?若是,请给出一种表示方式;若不是,请说明理由.
中的其他两项之积?若是,请给出一种表示方式;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在正三棱柱![]() 中,侧棱长
中,侧棱长![]() 为3,H、G分别是AB,
为3,H、G分别是AB,![]() 中点.
中点.

(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,求此三棱柱的侧面积;
,求此三棱柱的侧面积;
(3)若P为侧棱![]() 上一点,且
上一点,且![]() ,
,![]() 与平面
与平面![]() 所成角大小为
所成角大小为![]() ,求此三棱柱的体积.
,求此三棱柱的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com