Question

如图，在直四棱柱ABCD-A₁B₁C₁D₁中，AB=AD=2，DC=2

3

，AA₁=

3

，AD⊥DC，AC⊥BD垂足为E．
（Ⅰ）求证BD⊥A₁C；
（Ⅱ）求二面角A₁-BD-C₁的大小；
（Ⅲ）求异面直线AD与BC₁所成角的大小．

Answer 1

分析：解法一：
（1）在直四棱柱ABCD-AB₁C₁D₁中，由AA₁⊥底面ABCD可知：AC是A₁C在平面ABCD上的射影．因为BD⊥AC，所以BD⊥A₁C；
（2）二面角的度量关键在于作出它的平面角，常用的方法就是三垂线定理．连接A₁E，C₁E，A₁C₁．与（I）同理可证BD⊥A₁E，BD⊥C₁E，所以∠A₁EC₁为二面角A₁-BD-C₁的平面角；
（3）求异面直线所成的角，一般有两种方法，一种是几何法，其基本解题思路是“异面化共面，认定再计算”，即利用平移法和补形法将两条异面直线转化到同一个三角形中，结合余弦定理来求．还有一种方法是向量法，即建立空间直角坐标系，利用向量的代数法和几何法求解．本题采用的是“几何法”：过B作BF∥AD交AC于F，连接FC₁，则∠C₁BF就是AD与BC₁所成的角．
解法二：
（1）同解法一；
（2）以D为坐标原点，DA，DC，DD₁所在直线分别为x轴，y轴，z轴，建立空间直角坐标系．连接A₁E，C₁E，A₁C₁，与（1）同理可证，BD⊥A₁E，BD⊥C₁E，所以∠A₁EC₁为二面角A₁-ED-C₁的平面角．因为

EA

1⊥

EC1

，所以EA₁⊥EC₁．则二面角A₁-ED-C₁的大小为90°．
解法三：
（1）同解法一；
（2）建立空间直角坐标系，坐标原点为E．连接A₁E，C₁E，A₁C₁．与（Ⅰ）同理可证BD⊥A₁E，BD⊥C₁E，所以∠A₁EC₁为二面角A₁-BD-C₁的平面角．由E（0，0，0）A₁（0，-1，

3

），C₁（0，3，

3

）．因为

EA

1⊥

EC1

，所以EA₁⊥EC₁．则二面角A₁-ED-C₁的大小为90°．
解法二、三都是用的“向量法”，只是空间直角坐标系建立的位置不同，这样各个点的坐标也会随之改变．这种解法的好处就是：（1）解题过程中较少用到空间几何中判定线线、面面、线面相对位置的有关定理，因为这些可以用向量方法来解决．（2）即使立体感稍差一些的学生也可以顺利解出，因为只需画个草图以建立坐标系和观察有关点的位置即可．

解答：解：法一：
（I）在直四棱柱ABCD-AB₁C₁D₁中，
∵AA₁⊥底面ABCD．∴AC是A₁C在平面ABCD上的射影．
∵BD⊥AC．∴BD⊥A₁C；
（II）连接A₁E，C₁E，A₁C₁．
与（I）同理可证BD⊥A₁E，BD⊥C₁E，
∴∠A₁EC₁为二面角A₁-BD-C₁的平面角．
∵AD⊥DC，∴∠A₁D₁C₁=∠ADC=90°，
又A₁D₁=AD=2，D₁C₁=DC=2

3

，AA₁=

3

且AC⊥BD，
∴A₁C₁=4，AE=1，EC=3，∴A₁E=2，C₁E=2

3

，
在△A₁EC₁中，A₁C₁²=A₁E²+C₁E²，∴∠A₁EC₁=90°，
即二面角A₁-BD-C₁的大小为90°．

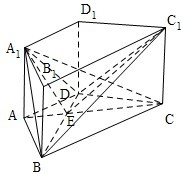
（III）过B作BF∥AD交AC于F，连接FC₁，
则∠C₁BF就是AD与BC₁所成的角．
∵AB=AD=2，BD⊥AC，AE=1，
∴BF=2，EF=1，FC=2，BC=DC，∴FC₁=

7

，BC₁=

15

，
在△BFC₁中，cos∠C₁BF=

15+4-7

1•2• 15

=

15

5

，∴∠C₁BF=arccos

15

5

即异面直线AD与BC₁所成角的大小为arccos

15

5

．
法二：
（Ⅰ）同解法一
（Ⅱ）如图，以D为坐标原点，DA，DC，DD₁所在直线分别为x轴，y轴，z轴，建立空间直角坐标系．

连接A₁E，C₁E，A₁C₁．
与（1）同理可证，BD⊥A₁E，BD⊥C₁E，
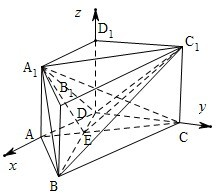
∴∠A₁EC₁为二面角A₁-ED-C₁的平面角．
由A₁（2，0，

3

）C₁（0，2

3

，

3

）E（

3

2

，

3

2

，0）
得

EA

1=（

1

2

，-

3

2

，

3

），

EC1

=（-

3

2

，

3 3

2

，

3

）
∴

EA

1•

EC1

=-

3

4

-

9

4

+3=0，
∴

EA

1⊥

EC1

，即EA₁⊥EC₁．
∴二面角A₁-ED-C₁的大小为90°
（Ⅲ）如图，由D（0，0，0），A（2，0，0），C₁（0，2

3

，

3

），B（3，

3

，0），
得

AD

=（-2，0，0），

BC1

=（-3，

3

，

3

），
∴

AD

•

BC1

=6，|

AD

|•

BC1

=6，|

AD

|=2，|

BC1

|=

15

∴cos（

AD

，

BC1

）=

AD ， BC1

| AD || BC1 |

=

6

2 15

=

15

5

，
∵异面直线AD与BC₁所成角的大小为arccos

15

5

．
法三：
（Ⅰ）同解法一．
（Ⅱ）如图，建立空间直角坐标系，坐标原点为E．连接A₁E，C₁E，A₁C₁．

与（Ⅰ）同理可证BD⊥A₁E，BD⊥C₁E，
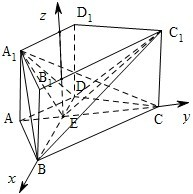
∴∠A₁EC₁为二面角A₁-BD-C₁的平面角．
由E（0，0，0）A₁（0，-1，

3

），C₁（0，3，

3

）．
得

EA1

（0，-1，

3

），

EC1

=（0，3，

3

）．
∵

EA1

•

EC1

=-3+3=0，
∴

EA1

⊥

EC1

即EA₁⊥EC₁，
∴二面角A₁-BD-C₁的大小为90°．

点评：本小题主要考查棱柱的结构特征，二面角和线面关系等基本知识，同时考查空间想象能力和推理、运算能力．