
若函数f(x)=kax-a-x(a>0且a≠1)在(-∞,+∞)上既是奇函数又是增函数,则函数g(x)=loga(x+k)的图象是
A.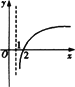
B.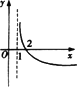
C.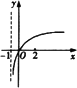
D.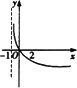
科目:高中数学 来源:训练必修四数学人教A版 人教A版 题型:044
已知平面向量a=(![]() ,-1),b=(
,-1),b=(![]() ,
,![]() ).
).
(1)证明a⊥b;
(2)若存在不同时为零的实数k、t,使得x=a+(t2-3)b,y=-ka+tb,且x⊥y,求函数关系式k=f(t).
查看答案和解析>>
科目:高中数学 来源:学习周报 数学 北师大课标高二版(选修2-2) 2009-2010学年 第35期 总第191期 北师大课标 题型:044
平面向量a=(![]() ,-1),b=(
,-1),b=(![]() ,
,![]() ),若存在不同时为0的实数k和t,使得x=a+(t2-3)b,y=-ka+tb,且x⊥y,试确定函数k=f(t)的单调区间.
),若存在不同时为0的实数k和t,使得x=a+(t2-3)b,y=-ka+tb,且x⊥y,试确定函数k=f(t)的单调区间.
查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学必修四2.4平面向量的数量积练习卷(二)(解析版) 题型:解答题
已知a=( ,-1),b=
,-1),b= .
.
(1)求证:a⊥b;
(2)若存在不同时为0的实数k和t,使x=a+(t-3)b,y=-ka+tb,且x⊥y,试求函数关系式k=f(t);
(3)求函数k=f(t)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知平面向量a=(![]() ,-1),b=(
,-1),b=(![]() ,
, ![]() ).
).
(1) 若存在实数k和t,便得x=a+(t2-3)b, y=-ka+tb,且x⊥y,试求函数的关系式k=f(t);
(2) 根据(1)的结论,确定k=f(t)的单调区间。
分析:利用向量知识转化为函数问题求解.
查看答案和解析>>
科目:高中数学 来源:浙江省杭州市西湖高级中学2011-2012学年高三10月月考试题数学理 题型:解答题
设函数f(x)=ka x- a-x(a>0且a≠1)是定义域为R的奇函数.
(1)求k值;
(2)若f(1)>0,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
(3)若f(1)=,且g(x)=a 2x+a - 2x-2m f(x) 在[1,+∞)上的最小值为-2,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com