
【题目】某种赌博每局的规则是:赌客先在标记有1,2,3,4,5的卡片中随机摸取一张,将卡片上的数字作为其赌金;随后放回该卡片,再随机摸取两张,将这两张卡片上数字之差的绝对值的1.4倍作为其奖金.若随机变量ξ1和ξ2分别表示赌客在一局赌博中的赌金和奖金,则D(ξ1)=_____,E(ξ1)﹣E(ξ2)=_____.
【答案】2 0.2
【解析】
分别求出随机变量ξ1和ξ2的分布列,根据期望和方差公式计算得解.
设a,b∈{1,2,3,4,5},则p(ξ1=a)![]() ,其ξ1分布列为:
,其ξ1分布列为:
ξ1 | 1 | 2 | 3 | 4 | 5 |
P |
|
|
|
|
|
E(ξ1)![]() (1+2+3+4+5)=3.
(1+2+3+4+5)=3.
D(ξ1)![]() [(1﹣3)2+(2﹣3)2+(3﹣3)2+(4﹣3)2+(5﹣3)2]=2.
[(1﹣3)2+(2﹣3)2+(3﹣3)2+(4﹣3)2+(5﹣3)2]=2.
ξ2=1.4|a﹣b|的可能取值分别为:1.4,2.8,4.2,5.6,
P(ξ2=1.4)![]() ,P(ξ2=2.8)
,P(ξ2=2.8)![]() ,P(ξ2=4.2)
,P(ξ2=4.2)![]() ,P(ξ2=5.6)
,P(ξ2=5.6)![]() ,可得分布列.
,可得分布列.
ξ2 | 1.4 | 2.8 | 4.2 | 5.6 |
P |
|
|
|
|
E(ξ2)=1.4![]() 2.8
2.8![]() 4.2
4.2![]() 5.6
5.6![]() 2.8.
2.8.
∴E(ξ1)﹣E(ξ2)=0.2.
故答案为:2,0.2.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为常数.
为常数.
(Ⅰ)若![]() 的图像在
的图像在![]() 处的切线经过点(3,4),求
处的切线经过点(3,4),求![]() 的值;
的值;
(Ⅱ)若![]() ,求证:
,求证: 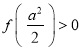 ;
;
(Ⅲ)当函数![]() 存在三个不同的零点时,求
存在三个不同的零点时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆M与直线![]() 相切,且与圆N:
相切,且与圆N:![]() 外切
外切
(1)求动圆圆心M的轨迹C的方程;
(2)点O为坐标原点,过曲线C外且不在y轴上的点P作曲线C的两条切线,切点分别记为A,B,当直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() 时,求证:直线
时,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查公司员工的饮食习惯与月收入之间的关系,随机抽取了30名员工,并制作了这30人的月平均收入的频率分布直方图和饮食指数表(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主).其中月收入4000元以上员工中有11人饮食指数高于70.
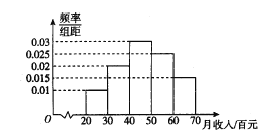
20 | 21 | 21 | 25 | 32 | 33 |
36 | 37 | 42 | 43 | 44 | 45 |
45 | 58 | 58 | 59 | 61 | 66 |
74 | 75 | 76 | 77 | 77 | 78 |
78 | 82 | 83 | 85 | 86 | 90 |
(1)是否有![]() 的把握认为饮食习惯与月收入有关系?若有,请说明理由,若没有,说明理由并分析原因;
的把握认为饮食习惯与月收入有关系?若有,请说明理由,若没有,说明理由并分析原因;
(2)从饮食指数在![]() 内的员工中任选2人,求他们的饮食指数均在
内的员工中任选2人,求他们的饮食指数均在![]() 内的概率;
内的概率;
(3)经调查某地若干户家庭的年收入![]() (万元)和年饮支出
(万元)和年饮支出![]() (万元)具有线性相关关系,并得到
(万元)具有线性相关关系,并得到![]() 关于
关于![]() 的回归直线方程:
的回归直线方程:![]() .若一个员工的月收入恰好为这30人的月平均收入,估计该人的年饮食支出费用.
.若一个员工的月收入恰好为这30人的月平均收入,估计该人的年饮食支出费用.
附: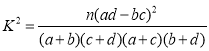 ,
,![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线E:y2=2px(p>0),焦点F到准线的距离为3,抛物线E上的两个动点A(x1,y1)和B(x2,y2),其中x1≠x2且x1+x2=4.线段AB的垂直平分线与x轴交于点 C.
(1)求抛物线E的方程;
(2)求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,两座建筑物AB,CD的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是10m和20m,从建筑物AB的顶部A看建筑物CD的视角∠CAD=60°.
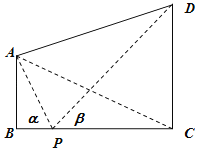
(1)求BC的长度;
(2)在线段BC上取一点P(点P与点B,C不重合),从点P看这两座建筑物的视角分别为∠APB=α,∠DPC=β,问点P在何处时,α+β最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司给年龄在![]() 岁的民众提供某种疾病的一年期医疗保险,现从
岁的民众提供某种疾病的一年期医疗保险,现从![]() 名参保人员中随机抽取
名参保人员中随机抽取![]() 名作为样本进行分析,按年龄段
名作为样本进行分析,按年龄段![]() 分成了五组,其频率分布直方图如下图所示;参保年龄与每人每年应交纳的保费如下表所示. 据统计,该公司每年为这一万名参保人员支出的各种费用为一百万元.
分成了五组,其频率分布直方图如下图所示;参保年龄与每人每年应交纳的保费如下表所示. 据统计,该公司每年为这一万名参保人员支出的各种费用为一百万元.
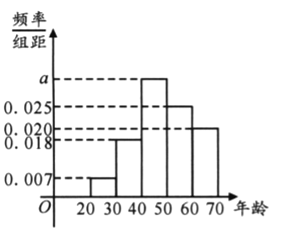
年龄 (单位:岁) |
|
|
|
|
|
保费 (单位:元) |
|
|
|
|
|
(1)用样本的频率分布估计总体分布,为使公司不亏本,求![]() 精确到整数时的最小值
精确到整数时的最小值![]() ;
;
(2![]() 之间的老人每
之间的老人每![]() 人中有
人中有![]() 人患该项疾病(以此频率作为概率).该病的治疗费为
人患该项疾病(以此频率作为概率).该病的治疗费为![]() 元,如果参保,保险公司补贴治疗费
元,如果参保,保险公司补贴治疗费![]() 元.某老人年龄
元.某老人年龄![]() 岁,若购买该项保险(
岁,若购买该项保险(![]() 取
取![]() 中的
中的![]() ).针对此疾病所支付的费用为
).针对此疾病所支付的费用为![]() 元;若没有购买该项保险,针对此疾病所支付的费用为
元;若没有购买该项保险,针对此疾病所支付的费用为![]() 元.试比较
元.试比较![]() 和
和![]() 的期望值大小,并判断该老人购买此项保险是否划算?
的期望值大小,并判断该老人购买此项保险是否划算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网店经销某商品,为了解该商品的月销量y(单位:千件)与售价x(单位:元/件)之间的关系,收集5组数据进行了初步处理,得到如下数表:
x | 5 | 6 | 7 | 8 | 9 |
y | 8 | 6 | 4.5 | 3.5 | 3 |
(1)统计学中用相关系数r来衡量两个变量之间线性相关关系的强弱,若![]() ,则认为相关性很强;若
,则认为相关性很强;若![]() ,则认为相关性一般;若
,则认为相关性一般;若![]() ,则认为相关性较弱.请根据上表数据计算y与x之间相关系数r,并说明y与x之间的线性相关关系的强弱(精确到0.01);
,则认为相关性较弱.请根据上表数据计算y与x之间相关系数r,并说明y与x之间的线性相关关系的强弱(精确到0.01);
(2)求y关于x的线性回归方程;
(3)根据(2)中的线性回归方程,应将售价x定为多少,可获取最大的月销售金额?(月销售金额=月销售量×当月售价)
附注:
参考数据:![]() ,
,
参考公式:相关系数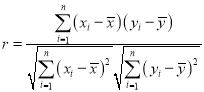 ,
,
线性回归方程![]() ,
, ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com