
【题目】已知点![]() (其中
(其中![]() ,点P的轨迹记为曲线
,点P的轨迹记为曲线![]() ,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点Q在曲线
,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点Q在曲线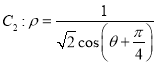 上.
上.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)当![]() ,
,![]() 时,求曲线
时,求曲线![]() 与曲线
与曲线![]() 的公共点的极坐标
的公共点的极坐标
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
【题目】已知极点为直角坐标系的原点,极轴为x轴正半轴且单位长度相同的极坐标系中曲线![]() ,
,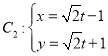 (t为参数).
(t为参数).
(1)求曲线![]() 上的点到曲线
上的点到曲线![]() 距离的最小值;
距离的最小值;
(2)若把![]() 上各点的横坐标都扩大到原来的2倍,纵坐标都扩大到原来的
上各点的横坐标都扩大到原来的2倍,纵坐标都扩大到原来的![]() 倍,得到曲线
倍,得到曲线![]() ,设
,设![]() ,曲线
,曲线![]() 与
与![]() 交于A,B两点,求
交于A,B两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下为简化的计划生育模型:每个家庭允许生男孩最多一个,即某一胎若为男孩,则不能再生下一胎,而女孩可以多个.为方便起见,此处约定每个家庭最多可生育3个小孩,即若第一胎或前两胎为女孩,则继续生,但若第三胎还是女孩,则不能再生了.设每一胎生男生女等可能,且各次生育相互独立.依据每个家庭最多生育一个男孩的政策以及我们对生育女孩的约定,令![]() 为某一家庭所生的女孩数,
为某一家庭所生的女孩数,![]() 为此家庭所生的男孩数.
为此家庭所生的男孩数.
(1)求![]() ,
,![]() 的分布列,并比较它们数学期望的大小;
的分布列,并比较它们数学期望的大小;
(2)求概率![]() ,其中
,其中![]() 为
为![]() 的方差.
的方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
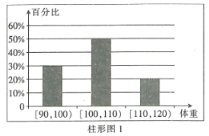
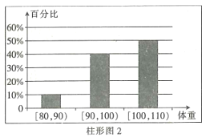
【题目】为了了解运动健身减肥的效果,某健身房调查了20名肥胖者,健身之前他们的体重(单位:![]() )情况如柱形图1所示,经过四个月的健身后,他们的体重情况如柱形图2所示.对比健身前后,关于这20名肥胖者,下面结论正确的是( )
)情况如柱形图1所示,经过四个月的健身后,他们的体重情况如柱形图2所示.对比健身前后,关于这20名肥胖者,下面结论正确的是( )
A.他们健身后,体重在区间![]() 内的人数增加了2个
内的人数增加了2个
B.他们健身后,体重在区间![]() 内的人数没有改变
内的人数没有改变
C.因为体重在![]() 内所占比例没有发生变化,所以说明健身对体重没有任何影响
内所占比例没有发生变化,所以说明健身对体重没有任何影响
D.他们健身后,原来体重在区间![]() 内的肥胖者体重都有减少
内的肥胖者体重都有减少
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,M,N,P分别是C1D1,BC,A1D1的中点,有下列四个结论:
①AP与CM是异面直线;②AP,CM,DD1相交于一点;③MN∥BD1;
④MN∥平面BB1D1D.
其中所有正确结论的编号是( )

A.①④B.②④C.①④D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com