
【题目】已知点F为抛物线E:y2=2px(p>0)的焦点,点A(2,m)在抛物线E上,且|AF|=3,

(1)求抛物线E的方程;
(2)已知点G(﹣1,0),延长AF交抛物线E于点B,证明:以点F为圆心且与直线GA相切的圆,必与直线GB相切.
【答案】(1)y2=4x;(2)证明见解析
【解析】
(1)由抛物线定义可得:|AF|=2![]() 3,解得p.即可得出抛物线E的方程.
3,解得p.即可得出抛物线E的方程.
(2)由点A(2,m)在抛物线E上,解得m,不妨取A![]() ,F(1,0),可得直线AF的方程,与抛物线方程联立化为2x2﹣5x+2=0,解得B
,F(1,0),可得直线AF的方程,与抛物线方程联立化为2x2﹣5x+2=0,解得B![]() .又G(﹣1,0),计算kGA,kGB,可得kGA+kGB=0,∠AGF=∠BGF,即可证明以点F为圆心且与直线GA相切的圆,必与直线GB相切.
.又G(﹣1,0),计算kGA,kGB,可得kGA+kGB=0,∠AGF=∠BGF,即可证明以点F为圆心且与直线GA相切的圆,必与直线GB相切.
解法一:(1)由抛物线定义可得:|AF|=2![]() 3,
3,
解得p=2.
∴抛物线E的方程为y2=4x;
(2)∵点A(2,m)在抛物线E上,
∴m2=4×2,
解得m![]() ,
,
不妨取A![]() ,F(1,0),
,F(1,0),
∴直线AF的方程:y=2![]() (x﹣1),
(x﹣1),
联立 ,化为2x2﹣5x+2=0,
,化为2x2﹣5x+2=0,
解得x=2或![]() ,B
,B![]() .
.
又G(﹣1,0),
∴kGA .kGB
.kGB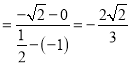 ,
,
∴kGA+kGB=0,
∴∠AGF=∠BGF,∴x轴平分∠AGB,
因此点F到直线GA,GB的距离相等,
∴以点F为圆心且与直线GA相切的圆,必与直线GB相切.
解法二:(1)同解法一.
(2)点A(2,m)在抛物线E上,
∴m2=4×2,解得m![]() ,不妨取A
,不妨取A![]() ,F(1,0),
,F(1,0),
∴直线AF的方程:y=2![]() (x﹣1),
(x﹣1),
联立 ,化为2x2﹣5x+2=0,
,化为2x2﹣5x+2=0,
解得x=2或![]() ,B
,B![]() .
.
又G(﹣1,0),
可得直线GA,GB的方程分别为:![]() x﹣3y+2
x﹣3y+2![]() 0,
0,![]() 0,
0,
点F(1,0)到直线GA的距离d ,
,
同理可得点F(1,0)到直线GB的距离![]() .
.
因此以点F为圆心且与直线GA相切的圆,必与直线GB相切.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间如下:
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
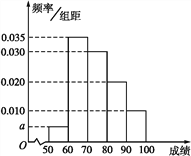
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知钝角△ABC中,∠B-∠C=90°,∠C=θ,其外接圆⊙O的半径为R.AD是⊙O的一条直径,过点D作⊙O的切线与BC的延长线交于H,过点D作BA的平行线交AC的延长线于E,交过D、O、H的圆于G,联结GH、EH.求△EGH的面积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() 为棱
为棱![]() 上的一点,且
上的一点,且![]() ,
,![]() 为棱
为棱![]() 的中点,
的中点,![]() 为棱
为棱![]() 上的一点,若
上的一点,若![]() 平面
平面![]() ,
,![]() 是边长为4的正三角形,
是边长为4的正三角形,![]() ,
,![]() .
.
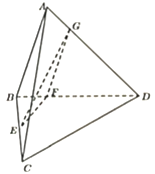
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),点
为参数),点![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)试判断点![]() 是否在直线
是否在直线![]() 上,并说明理由;
上,并说明理由;
(2)设直线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2021年开始,我省将试行“3+1+2“的普通高考新模式,即除语文、数学、外语3门必选科目外,考生再从物理、历史中选1门,从化学、生物、地理、政治中选2门作为选考科目.为了帮助学生合理选科,某中学将高一每个学生的六门科目综合成绩按比例均缩放成5分制,绘制成雷达图.甲同学的成绩雷达图如图所示,下面叙述一定不正确的是( )
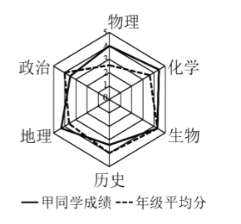
A.甲的物理成绩领先年级平均分最多
B.甲有2个科目的成绩低于年级平均分
C.甲的成绩从高到低的前3个科目依次是地理、化学、历史
D.对甲而言,物理、化学、地理是比较理想的一种选科结果
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日,某地援鄂医护人员
日,某地援鄂医护人员![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 人(其中
人(其中![]() 是队长)圆满完成抗击新冠肺炎疫情任务返回本地,他们受到当地群众与领导的热烈欢迎.当地媒体为了宣传他们的优秀事迹,让这
是队长)圆满完成抗击新冠肺炎疫情任务返回本地,他们受到当地群众与领导的热烈欢迎.当地媒体为了宣传他们的优秀事迹,让这![]() 名医护人员和接见他们的一位领导共
名医护人员和接见他们的一位领导共![]() 人站一排进行拍照,则领导和队长站在两端且
人站一排进行拍照,则领导和队长站在两端且![]() 相邻,而
相邻,而![]() 不相邻的排法种数为( )
不相邻的排法种数为( )
A.![]() 种B.
种B.![]() 种C.
种C.![]() 种D.
种D.![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两队进行篮球决赛,采取五场三胜制(当一队赢得三场胜利时,该队获胜,比赛结束).根据前期比赛成绩,甲队的主客场安排依次为“主主客客主”.设甲队主场取胜的概率为![]() ,客场取胜的概率为
,客场取胜的概率为![]() ,且各场比赛结果相互独立,则甲队不超过
,且各场比赛结果相互独立,则甲队不超过![]() 场即获胜的概率是( )
场即获胜的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com