
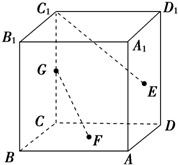
 如右图所示,正方体ABCD-A1B1C1D1中,E、F分别是正方形ADD1A1和ABCD的中心,G是CC1的中点,设GF、C1E与AB所成的角分别为α、β,则α+β等于( )
如右图所示,正方体ABCD-A1B1C1D1中,E、F分别是正方形ADD1A1和ABCD的中心,G是CC1的中点,设GF、C1E与AB所成的角分别为α、β,则α+β等于( )| A、120° | B、60° | C、75° | D、90° |
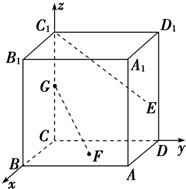 解:建立坐标系如图,
解:建立坐标系如图,| BA |
| GF |
| C1E |
| BA |
| GF |
| 1 | ||
|
| BA |
| C1E |
| ||
|
| 1 | ||
|
| ||
|
| 1 | ||
|


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
 将棱长相等的正方体按如右图所示的形状摆放,从上往下依次为第1层,第2层,第3层….则第2005层正方体的个数是( )
将棱长相等的正方体按如右图所示的形状摆放,从上往下依次为第1层,第2层,第3层….则第2005层正方体的个数是( )| A、4011 | B、4009 | C、2011015 | D、2009010 |
查看答案和解析>>
科目:高中数学 来源:2014届辽宁省大连市高一期末数学试卷 题型:选择题
如右图所示,正方体ABCD-A1B1C1D1中,点P在侧面BCC1B1及其边界上运动,并且总是保持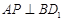 ,则动点P的轨迹是( )
,则动点P的轨迹是( )

A.线段B1C B.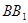 中点与
中点与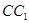 中点连成的线段
中点连成的线段
C.线段BC1 D.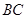 中点与
中点与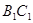 中点连成的线段
中点连成的线段
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 如右图所示,正方体ABCD-A1B1C1D1中,E、F分别是正方形ADD1A1和ABCD的中心,G是CC1的中点,设GF、C1E与AB所成的角分别为α、β,则α+β等于
如右图所示,正方体ABCD-A1B1C1D1中,E、F分别是正方形ADD1A1和ABCD的中心,G是CC1的中点,设GF、C1E与AB所成的角分别为α、β,则α+β等于查看答案和解析>>
科目:高中数学 来源:2011年高三数学第一轮复习巩固与练习:空间向量的应用(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com