
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的两焦点之间的距离为2,两条准线间的距离为8,直线l:y=k(x-m)(m∈R)与椭圆交于P,Q两点.
=1(a>b>0)的两焦点之间的距离为2,两条准线间的距离为8,直线l:y=k(x-m)(m∈R)与椭圆交于P,Q两点.
(1) 求椭圆C的方程;
(2) 设椭圆的左顶点为A,记直线AP,AQ的斜率分别为k1,k2.①若m=0,求k1k2的值;②若k1k2=-![]() ,求实数m的值.
,求实数m的值.
【答案】(1)![]() +
+![]() =1;(2)①-
=1;(2)①-![]() ,②m=1
,②m=1
【解析】
(1)题意说明![]() ,由这两个条件可求得椭圆方程;
,由这两个条件可求得椭圆方程;
(2)①设P(x0,y0),由于m=0,则Q(-x0,-y0),点在椭圆上得出![]() ,然后直接计算
,然后直接计算![]() 即得;
即得;
②由(1)得A(-2,0).设P(x1,y1),Q(x2,y2),直接方程与椭圆方程联立消元由韦达定理得![]() ,代入k1k2=
,代入k1k2=![]() ·
·![]() =
=![]() ·
·![]() ,整理后可求得
,整理后可求得![]() .
.
(1)因为椭圆C的两个焦点间距离为2,两准线间的距离为2×![]() =8,所以a=2,c=1,所以b2=3,
=8,所以a=2,c=1,所以b2=3,
所以椭圆的方程为![]() +
+![]() =1.
=1.
(2)①设P(x0,y0),由于m=0,则Q(-x0,-y0),
由![]() +
+![]() =1,得
=1,得![]() ,
,
所以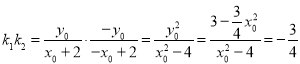 .
.
②由(1)得A(-2,0).
设P(x1,y1),Q(x2,y2),
联立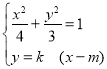 消去y,得(3+4k2)x2-8mk2x+4m2k2-12=0,
消去y,得(3+4k2)x2-8mk2x+4m2k2-12=0,
所以x1+x2=![]() ,x1·x2=
,x1·x2=![]() .
.
而k1k2=![]() ·
·![]() =
=![]() ·
·![]()
=![]()
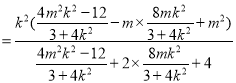 =-
=-![]() ,
,
化简得![]() =-
=-![]() ,即m2k2+mk2-2k2=0.
,即m2k2+mk2-2k2=0.
因为k2≠0,所以m2+m-2=0,解得m=1或m=-2(舍去).
当m=1时,Δ>0,所以,m=1.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】如图,已知直线![]() 交抛物线
交抛物线![]() 于
于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),过线段
左侧),过线段![]() (两端点除外)上的任意一点作直线
(两端点除外)上的任意一点作直线![]() ,使得直线
,使得直线![]() 与抛物线
与抛物线![]() 在点
在点![]() 处的切线平行,设直线
处的切线平行,设直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 、
、![]() 两点.
两点.
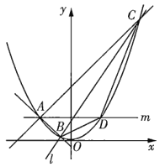
(1)记直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,证明:
,证明:![]() ;
;
(2)若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2014年非洲爆发了埃博拉病毒疫情,在疫情结束后,当地防疫部门做了一项回访调查,得到如下结果,
患病 | 不患病 | |
有良好卫生习惯 | 20 | 180 |
无良好卫生习惯 | 80 | 220 |
(1)结合上面列联表,是否有![]() 的把握认为是否患病与卫生习惯有关?
的把握认为是否患病与卫生习惯有关?
(2)现从有良好卫生习惯且不患病的180人中抽取![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共5人,再从这5人中选两人给市民做健康专题报告,求
共5人,再从这5人中选两人给市民做健康专题报告,求![]() ,
,![]() 至少有一人被选中的概率.
至少有一人被选中的概率.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
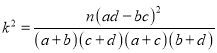
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() 的底面ABCD是边长为3的正方形,
的底面ABCD是边长为3的正方形,![]() 平面ABCD,
平面ABCD,![]() ,E为PD中点,过EB作平面
,E为PD中点,过EB作平面![]() 分别与线段PA、PC交于点M,N,且
分别与线段PA、PC交于点M,N,且![]() ,则
,则![]() ________;四边形EMBN的面积为________.
________;四边形EMBN的面积为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正四棱锥![]() 中,
中,![]() 是边长为3的等边三角形,点M是
是边长为3的等边三角形,点M是![]() 的重心,过点M作与平面PAC垂直的平面
的重心,过点M作与平面PAC垂直的平面![]() ,平面
,平面![]() 与截面PAC交线段的长度为2,则平面
与截面PAC交线段的长度为2,则平面![]() 与正四棱椎
与正四棱椎![]() 表面交线所围成的封闭图形的面积可能为______________.(请将可能的结果序号填到横线上)①2;②
表面交线所围成的封闭图形的面积可能为______________.(请将可能的结果序号填到横线上)①2;②![]() ;③3; ④
;③3; ④![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=2sinx(sinx![]() cosx)﹣1图象向右平移
cosx)﹣1图象向右平移![]() 个单位得函数g(x)的图象,则下列命题中正确的是( )
个单位得函数g(x)的图象,则下列命题中正确的是( )
A.f(x)在(![]() ,
,![]() )上单调递增
)上单调递增
B.函数f(x)的图象关于直线x![]() 对称
对称
C.g(x)=2cos2x
D.函数g(x)的图象关于点(![]() ,0)对称
,0)对称
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com