
分析 设f(x)=x2-2mx+4m2-6,则由题意可得f(0)=4m2-6<0,求得-$\sqrt{\frac{3}{2}}$<m<$\sqrt{\frac{3}{2}}$,再由韦达定理、二次函数的性质求得(α-1)2+(β-1)2取的范围.
解答 解:设f(x)=x2-2mx+4m2-6,则由题意可得f(0)=4m2-6<0,故有-$\sqrt{\frac{3}{2}}$<m<$\sqrt{\frac{3}{2}}$,
且由韦达定理可得 α+β=2m,α•β=4m2-6,
∴(α-1)2+(β-1)2=α2+β2-2(α+β)+2=(α+β)2-2αβ-2(α+β)+2
=4m2-2(4m2-6)-2•2m+2=-4m2-4m+14=-4${(m+\frac{1}{2})}^{2}$+15,
故当m=-$\frac{1}{2}$时,(α-1)2+(β-1)2取得最大值15;
当m趋于$\sqrt{\frac{3}{2}}$时,(α-1)2+(β-1)2 趋于5+4$\sqrt{6}$,
故(α-1)2+(β-1)2 趋的范围是(5+4$\sqrt{6}$,15].
点评 本题主要考查一元二次方程根的分布与系数的关系,二次函数的性质,体现了转化的数学思想,属于基础题.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
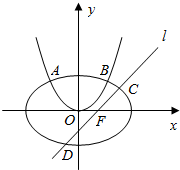 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的离心率是$\frac{\sqrt{2}}{2}$,椭圆和曲线E:x2=2py(p>0)相交于A、B两点,且M(-$\sqrt{2}$+1,2$\sqrt{2}$),B两点关于直线y=x+$\sqrt{2}$对称.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的离心率是$\frac{\sqrt{2}}{2}$,椭圆和曲线E:x2=2py(p>0)相交于A、B两点,且M(-$\sqrt{2}$+1,2$\sqrt{2}$),B两点关于直线y=x+$\sqrt{2}$对称.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
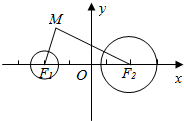 如图所示,已知定圆F1:x2+y2+10x+24=0,定圆F2:(x-5)2+y2=16,动圆M与定圆F1,F2都外切,求动圆圆心M的轨迹方程.
如图所示,已知定圆F1:x2+y2+10x+24=0,定圆F2:(x-5)2+y2=16,动圆M与定圆F1,F2都外切,求动圆圆心M的轨迹方程.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com