练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
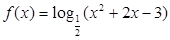
    函数的单调增区间是           .

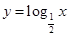
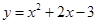
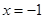
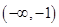
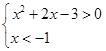
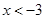
    试题分析：因为函数为减函数，且函数为开口向上，对称轴为，其单调递减区间，故由复合函数的单调性得，解得．故答案为．
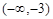
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    已知函数
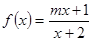
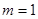
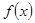
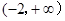
    （1）若，判断函数在上的单调性并用定义证明；
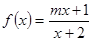
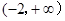
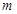
    （2）若函数在上是增函数，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

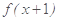
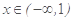
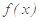
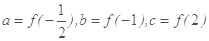
    已知函数是偶函数，当时，函数单调递减，设，则a，b，c的大小关系为（ 　）
    A．c<a<bB．a<b<cC．a<c<bD．c<b<a

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    函数的零点个数为（    ）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    下列函数在定义域上既是奇函数又是增函数的为（ ）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    函数是上的奇函数，、，，则的解集是（   ）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

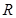
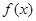
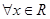
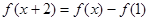
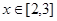
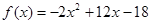
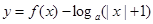
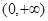
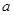
    定义域为的偶函数满足对，有，且当 时，，若函数在上至少有三个零点，则的取值范围是（   ）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

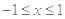
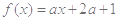
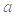
    若时，函数的值有正值也有负值，则的取值范围是(   )
    A．B．C．D．以上都不对

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

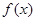
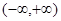
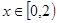
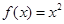
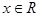
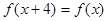
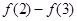
    已知函数是上的奇函数，时，，若对于任意，都有，则的值为         .

    查看答案和解析>>

    同步练习册答案