
【题目】已知函数![]() .
.
(1)当a为何值时,x轴为曲线![]() 的切线;
的切线;
(2)设函数![]() ,讨论
,讨论![]() 在区间(0,1)上零点的个数.
在区间(0,1)上零点的个数.
【答案】(1) ![]() (2)见解析
(2)见解析
【解析】
(1)求得![]() 的导数,设切点为
的导数,设切点为![]() ,可得
,可得![]() ,解方程可得所求值;(2)求
,解方程可得所求值;(2)求![]() 的解析式和导数,讨论当
的解析式和导数,讨论当![]() 时,当
时,当![]() 时,当
时,当![]() 时,结合函数的单调性和函数零点存在定理,即可得到所求零点个数.
时,结合函数的单调性和函数零点存在定理,即可得到所求零点个数.
(1)![]() 的导数为
的导数为![]() ,
,
设切点为![]() ,可得
,可得![]() ,
,
即![]() ,
,
解得![]() ;
;
(2)![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在(0,1)递增,可得
在(0,1)递增,可得
![]() ,
,![]() ,
,![]() 有一个零点;
有一个零点;
当![]() 时,
时,![]() ,
,![]() 在(0,1)递减,
在(0,1)递减,![]() ,
,
![]() 在(0,1)无零点;
在(0,1)无零点;
当![]() 时,
时,![]() 在(0,
在(0,![]() )递增,在(
)递增,在(![]() ,1)递减,
,1)递减,
可得![]() 在(0,1)的最大值为
在(0,1)的最大值为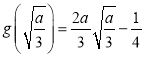 ,
,
①若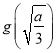 <0,即
<0,即![]() ,
,![]() 在(0,1)无零点;
在(0,1)无零点;
②若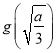 =0,即
=0,即![]() ,
,![]() 在(0,1)有一个零点;
在(0,1)有一个零点;
③若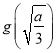 >0,即
>0,即![]() ,
,
当![]() 时,
时,![]() 在(0,1)有两个零点;
在(0,1)有两个零点;
当![]() 时,
时,![]() 在(0,1)有一个零点;
在(0,1)有一个零点;
综上可得,a<![]() 时,
时,![]() 在(0,1)无零点;
在(0,1)无零点;
当a=![]() 或a≥
或a≥![]() 时,
时,![]() 在(0,1)有一个零点;
在(0,1)有一个零点;
当![]() <a<
<a<![]() 时,
时,![]() 在(0,1)有两个零点.
在(0,1)有两个零点.


科目:高中数学 来源: 题型:
【题目】甲乙两人分别投掷两颗骰子与一颗骰子,设甲的两颗骰子的点数分别为![]() 与
与![]() ,乙的骰子的点数为
,乙的骰子的点数为![]() ,则掷出的点数满足
,则掷出的点数满足![]() 的概率为________(用最简分数表示).
的概率为________(用最简分数表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社会机构为了调查对手机游戏的兴趣与年龄的关系,通过问卷调查,整理数据得如下![]() 列联表:
列联表:

(1)根据列联表,能否有![]() 的把握认为对手机游戏的兴趣程度与年龄有关?
的把握认为对手机游戏的兴趣程度与年龄有关?
(2)若已经从40岁以上的被调查者中用分层抽样的方式抽取了10名,现从这10名被调查者中随机选取3名,记这3名被选出的被调查者中对手机游戏很有兴趣的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:![]()
参考数据:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场营销人员进行某商品M市场营销调查发现,每回馈消费者一定的点数,该商品每天的销量就会发生一定的变化,经过试点统计得到以下表:
反馈点数 | 1 | 2 | 3 | 4 | 5 |
销量(百件)/天 | 0. 5 | 0. 6 | 1 | 1. 4 | 1. 7 |
(1)经分析发现,可用线性回归模型拟合当地该商品销量![]() (百件)与返还点数
(百件)与返还点数![]() 之间的相关关系. 请用最小二乘法求
之间的相关关系. 请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测若返回6个点时该商品每天销量;
,并预测若返回6个点时该商品每天销量;
(2)若节日期间营销部对商品进行新一轮调整. 已知某地拟购买该商品的消费群体十分庞大,经营销调研机构对其中的200名消费者的返点数额的心理预期值进行了一个抽样调查,得到如下一份频数表:
返还点数预期值区间(百分比) |
|
|
|
|
|
|
频数 | 20 | 60 | 60 | 30 | 20 | 10 |
(ⅰ)求这200位拟购买该商品的消费者对返点点数的心理预期值![]() 的样本平均数及中位数的估计值(同一区间的预期值可用该区间的中点值代替;估计值精确到0. 1);
的样本平均数及中位数的估计值(同一区间的预期值可用该区间的中点值代替;估计值精确到0. 1);
(ⅱ)将对返点点数的心理预期值在![]() 和
和![]() 的消费者分别定义为“欲望紧缩型”消费者和“欲望膨胀型”消费者,现采用分层抽样的方法从位于这两个区间的30名消费者中随机抽取6名,再从这6人中随机抽取2名进行跟踪调查,设抽出的2人中,至少有一个人是“欲望膨胀型”消费者的概率是多少?
的消费者分别定义为“欲望紧缩型”消费者和“欲望膨胀型”消费者,现采用分层抽样的方法从位于这两个区间的30名消费者中随机抽取6名,再从这6人中随机抽取2名进行跟踪调查,设抽出的2人中,至少有一个人是“欲望膨胀型”消费者的概率是多少?
参考公式及数据:①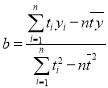 ,
,![]() ;②
;②![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是二次函数,且f(0)=0,f(x+1)=f(x)+x+1,
(1)求f(x)的表达式;
(2)若f(x)>a在x∈[﹣1,1]恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新能源汽车的春天来了!2018年3月5日上午,李克强总理做政府工作报告时表示,将新能源汽车车辆购置税优惠政策再延长三年,自2018年1月1日至2020年12月31日,对购置的新能源汽车免征车辆购置税.某人计划于2018年5月购买一辆某品牌新能源汽车,他从当地该品牌销售网站了解了近五个月的实际销量如下表:
月份 | 2017.12 | 2018.01 | 2018.02 | 2018.03 | 2018.04 |
月份编号 | 1 | 2 | 3 | 4 | 5 |
销量(万量) | 0.5 | 0.6 | 1 | 1.4 | 1.7 |
(1)经分析,可用线性回归模型拟合当地该品牌新能源汽车实际销量![]() (万辆)与月份编号
(万辆)与月份编号![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测2018年5月份当地该品牌新能源汽车的销量;
,并预测2018年5月份当地该品牌新能源汽车的销量;
(2)2018年6月12日,中央财政和地方财政将根据新能源汽车的最大续航里程(新能源汽车的最大续航里程是指理论上新能源汽车所装的燃料或电池所能够提供给车跑的最远里程)对购车补贴进行新一轮调整.已知某地拟购买新能源汽车的消费群体十分庞大,某调研机构对其中的200名消费者的购车补贴金额的心理预期值进行了一个抽样调查,得到如下一份频数表:
补贴金额预期值区间(万元) |
|
|
|
|
|
|
频数 | 20 | 60 | 60 | 30 | 20 | 10 |
(i)求这200位拟购买新能源汽车的消费者对补贴金额的心理预期值![]() 的方差
的方差![]() 及中位数的估计值(同一区间的预期值可用该区间的中点值代替,估计值精确到0.1);
及中位数的估计值(同一区间的预期值可用该区间的中点值代替,估计值精确到0.1);
(ii)将频率视为概率,现用随机抽样方法从该地区拟购买新能源汽车的所有消费者中随机抽取3人,记被抽取的3人中对补贴金额的心理预期值不低于3万元的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
附:①回归直线的斜率和截距的最小二乘估计公式分别为: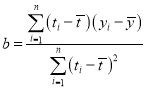 ,
,![]() ;②
;②![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com