
【题目】曲线C:ρ2﹣2ρcosθ﹣8=0 曲线E: ![]() (t是参数)
(t是参数)
(1)求曲线C的普通方程,并指出它是什么曲线.
(2)当k变化时指出曲线K是什么曲线以及它恒过的定点并求曲线E截曲线C所得弦长的最小值.
【答案】
(1)解:∵曲线C:ρ2﹣2ρcosθ﹣8=0,
∴x2+y2﹣2x﹣8=0,
∴(x﹣1)2+y2=9,
表示圆心(1,0)半径为3的圆
(2)解:曲线E: ![]() 消去参数得y﹣1=k(x﹣2)m是一条恒过定点(2,1)的直线(但不包括x=2),当直线E与圆心连线垂直时弦长最小,
消去参数得y﹣1=k(x﹣2)m是一条恒过定点(2,1)的直线(但不包括x=2),当直线E与圆心连线垂直时弦长最小,
设圆心到直线E的距离为d,则d= ![]() ,所以弦长的最小值=2
,所以弦长的最小值=2 ![]() =2
=2 ![]()

【解析】1、根据极坐标与直角坐标的公式转化可得x2+y2﹣2x﹣8=0,整理可得(x﹣1)2+y2=9。
2、首先消去参数可得,y﹣1=k(x﹣2)m是一条恒过定点(2,1)的直线,由题意可知当直线E与圆心连线垂直时弦长最小,利用圆的半径、弦长的一半、圆心到直线的距离构成的直角三角形可求出弦长的值。


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:
【题目】某地政府调查了工薪阶层1000人的月工资收入,并根据调查结果画出如图所示的频率分布直方图,其中工资收入分组区间是[10,15),[15,20),[20,25),[25,30)[30,35),[35,40](单位:百元)
(Ⅰ)为了了解工薪阶层对工资收入的满意程度,要用分层抽样的方法从调查的1000人中抽取100人做电话询问,求月工资收入在[30,35)内应抽取的人数;
(Ⅱ)根据频率分布直方图估计这1000人的平均月工资为多少元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若不等式2xlnx≥﹣x2+ax﹣3对x∈(0,+∞)恒成立,则实数a的取值范围是( )
A.(﹣∞,0)
B.(0,+∞)
C.(﹣∞,4]
D.[4,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二面角α﹣l﹣β为60°,ABα,AB⊥l,A为垂足,CDβ,C∈l,∠ACD=135°,则异面直线AB与CD所成角的余弦值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于空间直角坐标系O﹣xyz中的一点P(1,2,3),有下列说法:
①点P到坐标原点的距离为 ![]() ;
;
②OP的中点坐标为( ![]() );
);
③点P关于x轴对称的点的坐标为(﹣1,﹣2,﹣3);
④点P关于坐标原点对称的点的坐标为(1,2,﹣3);
⑤点P关于坐标平面xOy对称的点的坐标为(1,2,﹣3).
其中正确的个数是( )
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知长方形ABCD中,AB=2 ![]() ,AD=
,AD= ![]() ,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.
,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM. 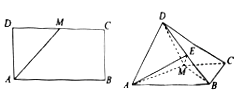
(1)求证:AD⊥BM;
(2)若点E是线段DB上的一动点,问点E在何位置时,二面角E﹣AM﹣D的余弦值为 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f (x)的导函数为f′(x),对任意x∈R都有f (x)>f′(x)成立,则( )
A.3f (ln2)<2 f (ln3)
B.3 f (ln2)=2 f (ln3)
C.3 f(ln2)>2 f (ln3)
D.3 f (ln2)与2 f (ln3)的大小不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列三个命题: ①若一个球的半径缩小到原来的 ![]() ,则其体积缩小到原来的
,则其体积缩小到原来的 ![]() ;
;
②若两组数据的平均数相等,则它们的标准差也相等;
③直线x+y+1=0与圆x2+y2= ![]() 相切.
相切.
其中真命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列五个命题:
①函数 ![]() 的一条对称轴是x=
的一条对称轴是x= ![]() ;
;
②函数y=tanx的图象关于点( ![]() ,0)对称;
,0)对称;
③正弦函数在第一象限为增函数;
④若 ![]() ,则x1﹣x2=kπ,其中k∈Z;
,则x1﹣x2=kπ,其中k∈Z;
⑤函数f(x)=sinx+2|sinx|,x∈[0,2π]的图象与直线y=k有且仅有两个不同的交点,则k的取值范围为(1,3).
以上五个命题中正确的有(填写所有正确命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com