
已知函数 ,
, ,
, .
.
(1)若 ,试判断并用定义证明函数
,试判断并用定义证明函数 的单调性;
的单调性;
(2)当 时,求证函数
时,求证函数 存在反函数.
存在反函数.
(1)增函数;(2)参考解析
解析试题分析:(1)当 时,
时,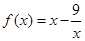 ,
, .通过函数的单调性的定义可证得函数
.通过函数的单调性的定义可证得函数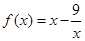 ,
, 单调递增.
单调递增.
(2)由 ,所以将x的区间分为两类即
,所以将x的区间分为两类即 和
和 .所以函数
.所以函数 .由(1)可得函数
.由(1)可得函数 是递增函数.应用单调性的定义同样可得函数
是递增函数.应用单调性的定义同样可得函数 是递增.根据反函数的定义可得函数存在反函数.
是递增.根据反函数的定义可得函数存在反函数.
试题解析:(1)判断:若 ,函数
,函数 在
在 上是增函数.
上是增函数.
证明:当 时,
时,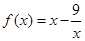 ,
, 在
在 上是增函数.2分
上是增函数.2分
在区间 上任取
上任取 ,设
,设 ,
,
所以 ,即
,即 在
在 上是增函数.6分
上是增函数.6分
(2)因为 ,所以
,所以 8分
8分
当 时,
时, 在
在 上是增函数,9分
上是增函数,9分
证明:当 时,
时, 在
在 上是增函数(过程略)11分
上是增函数(过程略)11分 在在
在在 上也是增函数,当
上也是增函数,当 时,
时,
 上是增函数12分
上是增函数12分
所以任意一个 ,均能找到唯一的
,均能找到唯一的 和它对应,
和它对应,
所以

 时,
时, 存在反函数14分
存在反函数14分
考点:1.函数的单调性.2.函数单调性的定义.3.反函数的概念.


科目:高中数学 来源: 题型:解答题
(2013•重庆)某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为r米,高为h米,体积为V立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为12000π元(π为圆周率).
(1)将V表示成r的函数V(r),并求该函数的定义域;
(2)讨论函数V(r)的单调性,并确定r和h为何值时该蓄水池的体积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知定义在R上的函数f(x)对任意实数x、y恒有f(x)+f(y)=f(x+y),且当x>0时,f(x)<0,又f(1)=- .
.
(1)求证:f(x)为奇函数;
(2)求证:f(x)在R上是减函数;
(3)求f(x)在[-3,6]上的最大值与最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com