
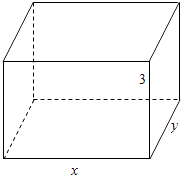
【题目】某单位建造一间背面靠墙的小房,地面面积为12m2 , 房屋正面每平方米造价为1200元,房屋侧面每平方米造价为800元,屋顶的造价为5800元,如果墙高为3m,且不计房屋背面和地面的费用,设房屋正面地面的边长为xm,房屋的总造价为y元.
(1)求y用x表示的函数关系式;
(2)怎样设计房屋能使总造价最低?最低总造价是多少?
【答案】
(1)解:如图所示,设底面的长为xm,宽ym,
则y= ![]() m.
m.
设房屋总造价为f(x),
由题意可得f(x)=3x1200+3× ![]() ×800×2+5800=3600(x+
×800×2+5800=3600(x+ ![]() )+5800(x>0)
)+5800(x>0)
(2)解:f(x)=3600(x+ ![]() )+5800≥28800+5800=34600,
)+5800≥28800+5800=34600,
当且仅当x=4时取等号.
答:当底面的长宽分别为4m,3m时,可使房屋总造价最低,总造价是34600元.
【解析】(1)设底面的长为xm,宽ym,则y= ![]() m.设房屋总造价为f(x),由题意可得f(x)=3x1200+3×
m.设房屋总造价为f(x),由题意可得f(x)=3x1200+3× ![]() ×800×2+5800=3600(x+
×800×2+5800=3600(x+ ![]() )+5800(x>0);(2)利用基本不等式即可得出结论.
)+5800(x>0);(2)利用基本不等式即可得出结论.
【考点精析】解答此题的关键在于理解基本不等式在最值问题中的应用的相关知识,掌握用基本不等式求最值时(积定和最小,和定积最大),要注意满足三个条件“一正、二定、三相等”.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直线)行驶.甲车、乙车的速度曲线分别为V甲和V乙(如图所示).那么对于图中给定的t0和t1 , 下列判断中一定正确的是( ) 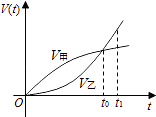
A.在t1时刻,甲车在乙车前面
B.t1时刻后,甲车在乙车后面
C.在t0时刻,两车的位置相同
D.t0时刻后,乙车在甲车前面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,分别求函数
时,分别求函数![]() 的最小值和
的最小值和![]() 的最大值,并证明当
的最大值,并证明当![]() 时,
时, ![]() 成立;
成立;
(3)令![]() ,当
,当![]() 时,判断函数
时,判断函数![]() 有几个不同的零点并证明.
有几个不同的零点并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O:x2+y2=r2(r>0),点P为圆O上任意一点(不在坐标轴上),过点P作倾斜角互补的两条直线分别交圆O于另一点A,B.
(1)当直线PA的斜率为2时,
①若点A的坐标为(﹣ ![]() ,﹣
,﹣ ![]() ),求点P的坐标;
),求点P的坐标;
②若点P的横坐标为2,且PA=2PB,求r的值;
(2)当点P在圆O上移动时,求证:直线OP与AB的斜率之积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B、C为三个锐角,且A+B+C=π,若向量 ![]() =(2sinA﹣2,cosA+sinA)与向量
=(2sinA﹣2,cosA+sinA)与向量 ![]() =(cosA﹣sinA,1+sinA)是共线向量. (Ⅰ)求角A;
=(cosA﹣sinA,1+sinA)是共线向量. (Ⅰ)求角A;
(Ⅱ)求函数y=2sin2B+cos ![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义平面向量之间的一种运算“⊙”如下:对任意的 ![]() ,令
,令 ![]() ,下面说法错误的是( )
,下面说法错误的是( )
A.若 ![]() 与
与 ![]() 共线,则
共线,则 ![]() ⊙
⊙ ![]() =0
=0
B.![]() ⊙
⊙ ![]() =
= ![]() ⊙
⊙ ![]()
C.对任意的λ∈R,有 ![]() ⊙
⊙ ![]() =
= ![]() ⊙
⊙ ![]() )
)
D.( ![]() ⊙
⊙ ![]() )2+(
)2+( ![]() )2=|
)2=| ![]() |2|
|2| ![]() |2
|2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=lnx,g(x)= ![]() x2+mx+
x2+mx+ ![]() (m<0),直线l与函数f(x)的图象相切,切点的横坐标为1,且直线l与函数g(x)的图象也相切.
(m<0),直线l与函数f(x)的图象相切,切点的横坐标为1,且直线l与函数g(x)的图象也相切.
(1)求直线l的方程及实数m的值;
(2)若h(x)=f(x)﹣x+3,求函数h(x)的最大值;
(3)当0<b<a时,求证:f(a+b)﹣f(2a)< ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com