
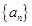 中,
中,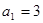 ,
,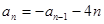 (
(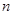 ≥2,且
≥2,且 ),数列
),数列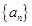 的前
的前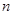 项和
项和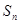 .
.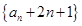 是等比数列,并求
是等比数列,并求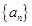 的通项公式;
的通项公式;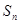 ;
;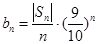 ,求
,求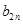 的最大值.
的最大值. ;(3)
;(3)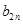 的最大值为
的最大值为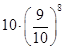 .
.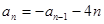 (
(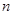 ≥2,且
≥2,且 ),
),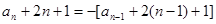 ,
, 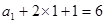 ,
,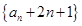 是首项为
是首项为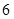 ,公比为
,公比为 的等比数列
的等比数列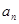 }的通项公式
}的通项公式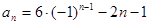 (
( ),
),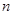 时偶数时,
时偶数时,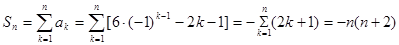 ,
,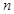 是奇数时,
是奇数时,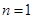 ,则
,则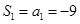
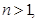 则
则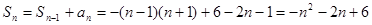
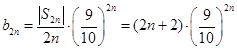 ,
, 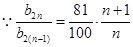 ,
,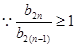 ,得
,得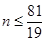 ,由于
,由于 ,
,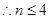 ,
, 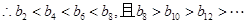
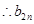 的最大值为
的最大值为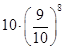
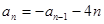 (
(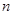 ≥2,且
≥2,且 ),
),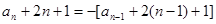 , ……………2分
, ……………2分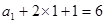 ,
,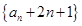 是首项为
是首项为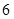 ,公比为
,公比为 的等比数列, ……………4分
的等比数列, ……………4分 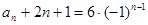 ,
,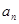 }的通项公式为
}的通项公式为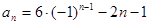 (
(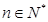 ); ……………6分
); ……………6分 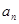 }的通项公式
}的通项公式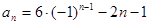 (
( ),
),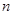 时偶数时,
时偶数时,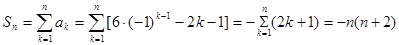 , ……………8分
, ……………8分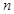 是奇数时,
是奇数时,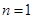 ,则
,则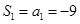
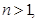 则
则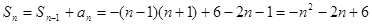 ,………10分
,………10分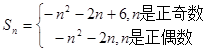 ; ……………11分
; ……………11分 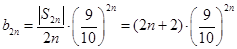 , ……………12分
, ……………12分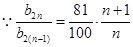 ,
,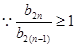 ,得
,得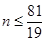 ,由于
,由于 ,
,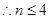 , ……………14分
, ……………14分 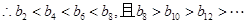
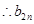 的最大值为
的最大值为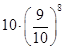 ……………16分
……………16分 

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com