
【题目】拉丁舞,又称拉丁风情舞或自由社交舞,它是拉丁人民在漫长的历史长河中形成的,包含伦巴、恰恰、牛仔舞、桑巴、斗牛舞、深受人民的喜爱.某艺术培训机构为了调查本校学院对拉丁舞的学习情况,分别在刚学习了一个季度的本校大班(8岁以下)及种子班(8岁以上)的学员中各随机抽取了15名学员进行摸底考试,这30名学员考试成绩的茎叶图如图所示.

规定:成绩不低于85分,则认为成绩优秀;成绩低于85分,则认为成绩一般.
(1)根据上述数据填写下列2×2联表:
成绩优秀 | 成绩一般 | 总计 | |
大班 | |||
种子班 | |||
总计 |
判断是否有95%的把握认为成绩优秀或成绩一般与学员的年龄有关;
(2)在大班及种子班的参加摸底考试且成绩优秀的学员中以分层抽样的方式抽取6名学员进行特别集训,集训后,再对这6名学员进行测试,按测试成绩,取前3名授予“舞蹈小精灵”称号,在被授予“舞蹈小精灵”称号的学员中,求种子班的学员恰好有2人的概率.
参考公式及数据: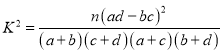 ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
【答案】(1)列联表见解析,有;(2)![]() .
.
【解析】
(1)先阅读题意,再分析数据,填写列联表即可;
(2)由茎叶图中的数据,分别列出所求事件的基本事件,然后结合古典概型概率公式求解即可.
解:(1)由茎叶图的数据,填写2×2列联表如下:
成绩优秀 | 成绩一般 | 总计 | |
大班 | 6 | 9 | 15 |
种子班 | 12 | 3 | 15 |
总计 | 18 | 12 | 30 |
根据列联表中的数据,得到![]()
因此有95%的把握认为成绩优秀或成绩一般与学员的年龄有关.
(2)由茎叶图中的数据可知,大班学员中成绩优秀的人数为6,种子班学员中成绩优秀的人数为12,以分层抽样的方式抽取6人,则大班抽取的人数为![]() ,记为
,记为![]() ,
,
种子班抽取的人数为![]() ,记为
,记为![]() ,
,
则被授予“舞蹈小精灵”称号的基本事件有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共20个,
,共20个,
其中种子班学员的人数恰有2人的基本时间有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共12个,
,共12个,
故被授予“舞蹈小精灵”称号的学员中,求种子班的学员恰好有2人的概率为![]() .
.


 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】为了美化校园,要对校园内某一区域作如下设计,如图,已知![]() ,
,![]() ,
,![]() ,在边BC上选一点P. 沿着AP和CP重新栽种花木,图中阴影部分铺上草坪. AP段栽种花木费用是每米3a元,CP段栽种花木费用是每米2a元,其中a是正常数.设
,在边BC上选一点P. 沿着AP和CP重新栽种花木,图中阴影部分铺上草坪. AP段栽种花木费用是每米3a元,CP段栽种花木费用是每米2a元,其中a是正常数.设![]() .
.
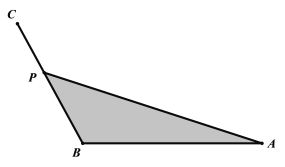
(1)求栽种花木费用y关于θ的函数表达式;
(2)求![]() 的值,使得栽种花木费用y最小.
的值,使得栽种花木费用y最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 是公差为d(
是公差为d(![]() )的等差数列,它的前n项和记为
)的等差数列,它的前n项和记为![]() ,数列
,数列![]() 是公比为q(
是公比为q(![]() )的等比数列,它的前n项和记为
)的等比数列,它的前n项和记为![]() .若
.若![]() ,且存在不小于3的正整数
,且存在不小于3的正整数![]() ,使
,使![]() .
.
(1)若![]() ,求
,求![]() .
.
(2)若![]() 试比较
试比较![]() 与
与![]() 的大小,并说明理由;
的大小,并说明理由;
(3)若![]() ,是否存在整数m,k,使
,是否存在整数m,k,使![]() 若存在,求出m,k的值;若不存在,说明理由.
若存在,求出m,k的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知直线
中,已知直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以直角坐标系原点为极点,
为参数),以直角坐标系原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 和直线
和直线![]() 的极坐标方程;
的极坐标方程;
(2)已知直线![]() 与曲线
与曲线![]() 、
、![]() 相交于异于极点的点
相交于异于极点的点![]() ,若
,若![]() 的极径分别为
的极径分别为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面为直角梯形,
的底面为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,二面角
,二面角![]() 的大小为
的大小为![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,![]() 为线段
为线段![]() 上的动点.
上的动点.
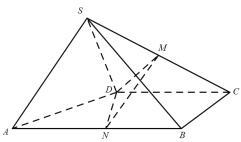
(1)求证:平面![]() 平面
平面![]() ;
;
(2)是否存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ,若存在,求
,若存在,求![]() 的值,不存在说出理由.
的值,不存在说出理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() ,若
,若![]() .
.
⑴ 求函数![]() 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
⑵ 将函数![]() 的图象上各点的横坐标伸长为原来的
的图象上各点的横坐标伸长为原来的![]() 倍(纵坐标不变),再将得到的图象向左平移
倍(纵坐标不变),再将得到的图象向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,求函数
的图象,求函数![]() 在
在![]() 上的最小值.
上的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com