
【题目】金砖国家领导人第九次会晤于2017年9月3日至5日在中国福建厦门市举行,为了在金砖峰会期间为来到厦门的外国嘉宾提供服务,培训部对两千余名志愿者进行了集中培训,为了检验培训效果,现培训部从两千余名志愿者中随机抽取100名,按年龄(单位:岁)分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
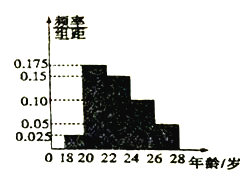
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者前去机场参加接待外宾礼仪测试,则应从第3,4,5组中各抽取多少名志愿者?
(2)在(1)的条件下,若在第3,4组的志愿者中随机抽取2名志愿者介绍接待外宾经验感受,求第4组至少有1名志愿者被抽中的概率.
【答案】(1)应从第3,4,5组中分别抽取3名,2名,1名志愿者; (2)![]() .
.
【解析】试题分析:(1)现有频率分布直方图,求得第![]() 组的频数,再利用分层抽样的方法得到结果;
组的频数,再利用分层抽样的方法得到结果;
(2)根据古典概型的概率计算公式,即可求解第4组至少有1名志愿者的概率.
试题解析:
(1)第3组的人数为![]() ,
,
第4组的人数为![]()
第5组的人数为![]() .
.
因为第3,4,5组共有60名志愿者,所以利用分层抽样的方法在60名志愿者中抽,56名志愿者,每组抽取的人数分别为,第3组: ![]() ,第4组:
,第4组: ![]() ,第5组:
,第5组: ![]() .
.
所以应从第3,4,5组中分别抽取3名,2名,1名志愿者.
(2)记第3组的3名志愿者分别为![]() ,
, ![]() ,
, ![]() ,第4组的2名志愿者分别为
,第4组的2名志愿者分别为![]() ,
, ![]() ,则从透明志愿者中抽取2名志愿者的情况有
,则从透明志愿者中抽取2名志愿者的情况有![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,共10种.
,共10种.
其中第4组的2名志愿者![]() ,
, ![]() 至少有1名被抽中的情况有
至少有1名被抽中的情况有![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,共7种.
,共7种.
所以第4组至少有1名志愿者被抽中的概率为![]() .
.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx和g(x)=m(x2-1)(m∈R).
(1)m=1时,求方程f(x)=g(x)的实根;
(2)若对任意的x∈(1,+∞),函数y=g(x)的图象总在函数y=f(x)图象的上方,求m的取值范围;
(3)求证: ![]() +
+![]() +…+
+…+![]() >ln(2n+1) (n∈N*).
>ln(2n+1) (n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四边形![]() 的四个顶点在椭圆
的四个顶点在椭圆![]() :
: ![]() 上,对角线
上,对角线![]() 所在直线的斜率为
所在直线的斜率为![]() ,且
,且![]() ,
, ![]() .
.
(1)当点![]() 为椭圆
为椭圆![]() 的上顶点时,求
的上顶点时,求![]() 所在直线方程;
所在直线方程;
(2)求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
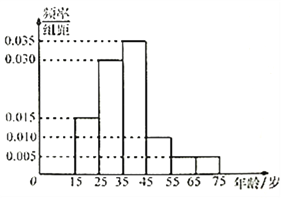
【题目】2017年5月14日,第一届“一带一路”国际高峰论坛在北京举行,为了解不同年龄的人对“一带一路”关注程度,某机构随机抽取了年龄在![]() 岁之间的100人进行调查,并按年龄绘制成频率分布直方图,如图所示,其分组区间为:
岁之间的100人进行调查,并按年龄绘制成频率分布直方图,如图所示,其分组区间为: ![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .把年龄落在区间
.把年龄落在区间![]() 和
和![]() 内的人分别称为“青少年”和“中老年”.
内的人分别称为“青少年”和“中老年”.
(1)根据频率分布直方图求样本的中位数(保留两位小数)和众数
(2)根据已知条件完成下面的2×2列联表,并判断能否有99%的把握认为关注“带一路”是否和年龄段有关?
关注 | 不关注 | 合计 | |
青少年 | 15 | ||
中老年 | |||
合计 | 50 | 50 | 100 |
附:参考公式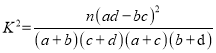 ,其中
,其中![]()
临界值表:
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年5月14日,第一届“一带一路”国际高峰论坛在北京举行,为了解不同年龄的人对“一带一路”关注程度,某机构随机抽取了年龄在15-75岁之间的100人进行调查, 经统计“青少年”与“中老年”的人数之比为9:11
关注 | 不关注 | 合计 | |
青少年 | 15 | ||
中老年 | |||
合计 | 50 | 50 | 100 |
(1)根据已知条件完成上面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为关注“一带一路”是否和年龄段有关?
的把握认为关注“一带一路”是否和年龄段有关?
(2)现从抽取的青少年中采用分层抽样的办法选取9人进行问卷调查.在这9人中再选取3人进行面对面询问,记选取的3人中关注“一带一路”的人数为X,求X的分布列及数学期望.
附:参考公式 ,其中
,其中![]()
临界值表:
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com