
【题目】如图,在四棱锥E﹣ABCD中,底面ABCD是矩形,AB=1,AE⊥平面CDE, ![]() ,F为线段DE上的一点.
,F为线段DE上的一点. 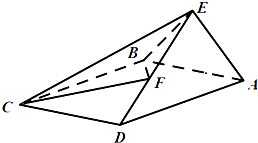
(1)求证:平面AED⊥平面ABCD;
(2)若二面角E﹣BC﹣F与二面角F﹣BC﹣D的大小相等,求DF的长.
【答案】
(1)证明:∵AE⊥面CDE,CD面CDE,
∴AE⊥CD,
又∴ ![]() 是矩形,
是矩形,
∴AD⊥CD,∴CD⊥面AED,
又∵CD面ABCD,
∴平面AED⊥平面ABCD.
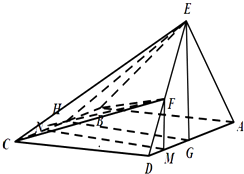
(2)解:取AD,BC的中点G,H,
连结EG,GH,EH,过F作FM||EG交AD于M,
过M作NM||HG交BC于N,连结FN,
∵ ![]() ,∴
,∴ ![]() 且EG⊥AD,
且EG⊥AD,
∵平面AED⊥平面ABCD,∴EG⊥面ABCD,GH⊥BC,
∴EH⊥BC,∴∠EHG就是二面角E﹣BC﹣D的平面角,
同理∠FNM就是二面角F﹣BC﹣D的平面角,
由题意得∠EHG=2∠FNM,
而 ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() .
.
【解析】(1)推导出AE⊥CD,AD⊥CD,从而CD⊥面AED,由此能证明平面AED⊥平面ABCD.(2)取AD,BC的中点G,H,连结EG,GH,EH,过F作FM||EG交AD于M,过M作NM||HG交BC于N,连结FN,推导出∠EHG就是二面角E﹣BC﹣D的平面角,∠FNM就是二面角F﹣BC﹣D的平面角,由此能求出DF的长.
【考点精析】关于本题考查的平面与平面垂直的判定,需要了解一个平面过另一个平面的垂线,则这两个平面垂直才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】△ABC的内角A、B、C所对的边分别为a,b,c. (Ⅰ)若a,b,c成等差数列,证明:sinA+sinC=2sin(A+C);
(Ⅱ)若a,b,c成等比数列,且c=2a,求cosB的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年中国(云南赛区)三对三篮球联赛在昆明市体育局的大力支持下,圆满顺利结束.组织方统计了来自![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 球队的男子的平均身高与本次比赛的平均得分,如下表所示:
球队的男子的平均身高与本次比赛的平均得分,如下表所示:
球队 |
|
|
|
|
|
平均身高 | 170 | 174 | 176 | 181 | 179 |
平均得分 | 62 | 64 | 66 | 70 | 68 |
(2)若![]() 队平均身高为
队平均身高为![]()
![]() ,根据(1)中所求得的回归方程,预测
,根据(1)中所求得的回归方程,预测![]() 队的平均得分.(精确到个位)
队的平均得分.(精确到个位)
注:回归方程![]() 中斜率和截距最小二乘估计公式分别为
中斜率和截距最小二乘估计公式分别为
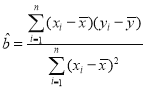 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,设边a,b,c所对的角为A,B,C,且A,B,C都不是直角,(bc﹣8)cosA+accosB=a2﹣b2 .
(1)若b+c=5,求b,c的值;
(2)若 ![]() ,求△ABC面积的最大值.
,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣1,g(x)=﹣x2+4x﹣3,若有f(a)=g(b),则b的取值范围为( )
A.![]()
B.(2﹣ ![]() ,2+
,2+ ![]() )
)
C.[1,3]
D.(1,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在公差为d的等差数列{an}中,已知a1=10,5a1a3=(2a2+2)2 .
(1)求d和an的值;
(2)若d<0,求|a1|+|a2|+|a3|+…+|a2021|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年11月,第十一届中国(珠海)国际航空航天博览会开幕式当天,歼-20的首次亮相给观众留下了极深的印象.某参赛国展示了最新研制的两种型号的无人机,先从参观人员中随机抽取100人对这两种型号的无人机进行评价,评价分为三个等级:优秀、良好、合格.由统计信息可知,甲型号无人机被评为优秀的频率为![]() 、良好的频率为
、良好的频率为![]() ;乙型号无人机被评为优秀的频率为
;乙型号无人机被评为优秀的频率为![]() ,且被评为良好的频率是合格的频率的5倍.
,且被评为良好的频率是合格的频率的5倍.
(1) 求这100人中对乙型号无人机评为优秀和良好的人数;
(2) 如果从这100人中按对甲型号无人机的评价等级用分层抽样的方法抽取5人,然后从其他对乙型号无人机评优秀、良好的人员中各选取1人进行座谈会,会后从这7人中随机抽取2人进行现场操作体验活动,求进行现场操作体验活动的2人都评优秀的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com