【题目】已知直线l在x轴上的截距比在y轴上的截距大1，且过点(6，-2)，求直线l的方程.
【答案】y=-
x+2或y=-
x+1.
【解析】试题分析：根据题干条件知道过点(6，-2)，可设直线l的点斜式方程为y+2=k(x-6)，分别求出直线的截距，在x轴上的截距比在y轴上的截距大1，故得
-(-6k-2)=1，从而求出k值。
方法一：设直线l的点斜式方程为y+2=k(x-6)(k≠0).
令x=0，得y=-6k-2；令y=0，
得x=
+6.
于是
-(-6k-2)=1，
解得k1=-
或k2=-
.
故直线l的方程为y+2=-
(x-6)或y+2=-
(x-6)，即y=-
x+2或y=-
x+1.
方法二：设直线l的斜截式方程为y=kx+b.
令y=0，得x=-
.
依题意，得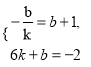
或
故直线l的方程为y=-
x+1或y=-
x+2.
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源： 题型：
【题目】如图，直三棱柱ABC﹣A1B1C1中，AB=AC=AA1 ， AB⊥AC，M是CC1的中点，N是BC的中点，点P在线段A1B1上运动．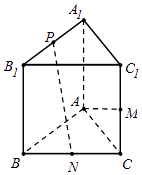 
（Ⅰ）求证：PN⊥AM；
（Ⅱ）试确定点P的位置，使直线PN和平面ABC所成的角最大．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在直角梯形ABCD中，BC⊥DC，AE⊥DC，M，N分别是AD，BE的中点，将三角形ADE沿AE折起，则下列说法正确的是________(填序号)．
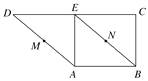
①不论D折至何位置(不在平面ABC内)，都有MN∥平面DEC；②不论D折至何位置，都有MN⊥AE；③不论D折至何位置(不在平面ABC内)，都有MN∥AB；④在折起过程中，一定存在某个位置，使EC⊥AD.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=alnx+（x﹣c）|x﹣c|，a＜0，c＞0 （Ⅰ）当 
时，求函数f（x）的单调区间；
（Ⅱ）设函数f（x）的图象在点P（x1 ， f（x1）），Q（x2 ， f（x2））两处的切线分别为l1 ， l2 ． 若 
，且l1⊥l2 ， 求实数c的最小值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
