
【题目】设α,β,γ为两两不重合的平面,l,m,n为两两不重合的直线,给出下列四个命题:
(1)若α⊥γ,β⊥γ,则α//β;
(2)若m![]() α,n
α,n![]() α,
α,![]() , 则α//β;
, 则α//β;
(3)若α//β,l![]() α,则l//β;
α,则l//β;
(4)若![]() , l//γ,则m//n.
, l//γ,则m//n.
其中正确的命题是( )
A.(1)(3)
B.(2)(3)
C.(2)(4)
D.(3)(4)
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,内角A,B,C的对边分别为a,b,c,且2asinB= ![]() b.
b.
(1)求角A的大小;
(2)若a=2,b+c=4,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费用支出x万元与销售额y万元之间有如下的对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计广告费用为12万元时,销售收入y的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线C:x2=2py(p>0)的焦点为F,准线为l,A∈C,已知以F为圆心,FA为半径的圆F交l于B,D两点;
(1)若∠BFD=90°,△ABD的面积为 ![]() ,求p的值及圆F的方程;
,求p的值及圆F的方程;
(2)若A,B,F三点在同一直线m上,直线n与m平行,且n与C只有一个公共点,求坐标原点到m,n距离的比值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知已知圆![]() 经过
经过 ![]() 、
、![]() 两点,且圆心C在直线
两点,且圆心C在直线 ![]() 上,求解:(1)圆C的方程;(2)若直线
上,求解:(1)圆C的方程;(2)若直线 ![]() 与圆
与圆 ![]() 总有公共点,求实数
总有公共点,求实数 ![]() 的取值范围.
的取值范围.
(1)求圆C的方程;
(2)若直线 ![]() 与圆
与圆 ![]() 总有公共点,求实数
总有公共点,求实数 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱A1B1C1D1﹣ABCD中,当底面四边形ABCD满足条件 时,有A1C⊥B1D1 . (注:填上你认为正确的一种条件即可,不必考虑所有可能的情形.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱台ABC﹣DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.
(1)求证:BF⊥平面ACFD;
(2)求直线BD与平面ACFD所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AC=3,BC=4,AB=5,点D是AB的中点. 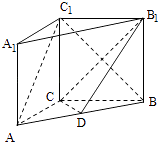
(1)求证:AC⊥BC1;
(2)求证:AC1∥平面CDB1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3﹣6x2+9x,g(x)= ![]() x3﹣
x3﹣ ![]() x2+ax﹣
x2+ax﹣ ![]() (a>1)若对任意的x1∈[0,4],总存在x2∈[0,4],使得f(x1)=g(x2),则实数a的取值范围为( )
(a>1)若对任意的x1∈[0,4],总存在x2∈[0,4],使得f(x1)=g(x2),则实数a的取值范围为( )
A.(1, ![]() ]
]
B.[9,+∞)??
C.(1, ![]() ]∪[9,+∞)
]∪[9,+∞)
D.[ ![]() ,
, ![]() ]∪[9,+∞)
]∪[9,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com