
【题目】已知数列{an}的首项a1=a,Sn是数列{an}的前n项和,且满足: ![]() =3n2an+
=3n2an+![]() ,an≠0,n≥2,n∈N*.
,an≠0,n≥2,n∈N*.
(1)若数列{an}是等差数列,求a的值;
(2)确定a的取值集合M,使a∈M时,数列{an}是递增数列.
【答案】(1)3(2)![]()
【解析】试题分析:(1)数列{an}是等差数列,故可从特殊情形出发:先求出a2=12-2a,a3=3+2a.再利用a1+a3=2a2,解得a=3.最后验证.(2)先由通项与和项关系,将已知条件转化为递推关系:an+1+an=6n+3,(n≥2).an+2-an=6,(n≥2),即数列a2,a4,a6, ,及数列a3,a5,a7, 都是公差为6的等差数列,要使数列{an}是递增数列,须有a1<a2![]() ,解得
,解得![]() <a<
<a<![]() .
.
试题解析:(1)在![]() =3n2an+
=3n2an+![]() 中分别令n=2,n=3,及a1=a得
中分别令n=2,n=3,及a1=a得
(a+a2)2=12a2+a2,(a+a2+a3)2=27a3+(a+a2)2,
因an≠0,所以a2=12-2a,a3=3+2a. 2分
因数列{an}是等差数列,所以a1+a3=2a2,即2(12-2a)=a+3+2a,解得a=3. 4分
经检验a=3时,an=3n,Sn=![]() ,Sn-1=
,Sn-1=![]() 满足
满足![]() =3n2an+
=3n2an+![]()
(2)由![]() =3n2an+
=3n2an+![]() ,得
,得![]() -
-![]() =3n2an,即(Sn+Sn-1)(Sn-Sn-1)=3n2an,
=3n2an,即(Sn+Sn-1)(Sn-Sn-1)=3n2an,
即(Sn+Sn-1)an=3n2an,因为an≠0,所以Sn+Sn-1=3n2,(n≥2),① 6分
所以Sn+1+Sn=3(n+1)2,②
②-①,得an+1+an=6n+3,(n≥2).③ 8分
所以an+2+an+1=6n+9,④
④-③,得an+2-an=6,(n≥2)
即数列a2,a4,a6, ,及数列a3,a5,a7, 都是公差为6的等差数列, 10分
因为a2=12-2a,a3=3+2a.
所以an=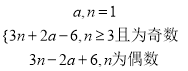 12分
12分
要使数列{an}是递增数列,须有
a1<a2,且当n为大于或等于3的奇数时,an<an+1,且当n为偶数时,an<an+1,
即a<12-2a,
3n+2a-6<3(n+1)-2a+6(n为大于或等于3的奇数),
3n-2a+6<3(n+1)+2a-6(n为偶数),
解得![]() <a<
<a<![]() .所以M=
.所以M=![]() ,当a∈M时,数列{an}是递增数列. 16分
,当a∈M时,数列{an}是递增数列. 16分


科目:高中数学 来源: 题型:
【题目】【2017广东佛山二模】已知椭圆![]() :
: ![]() (
(![]() )的焦距为4,左、右焦点分别为
)的焦距为4,左、右焦点分别为![]() 、
、![]() ,且
,且![]() 与抛物线
与抛物线![]() :
: ![]() 的交点所在的直线经过
的交点所在的直线经过![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
, ![]() 两点,与抛物线
两点,与抛物线![]() 无公共点,求
无公共点,求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},{bn},Sn为数列{an}的前n项和,向量 ![]() =(1,bn),
=(1,bn), ![]() =(an﹣1,Sn),
=(an﹣1,Sn), ![]() ∥
∥ ![]() .
.
(1)若bn=2,求数列{an}通项公式;
(2)若bn= ![]() ,a2=0.
,a2=0.
①证明:数列{an}为等差数列;
②设数列{cn}满足cn= ![]() ,问是否存在正整数l,m(l<m,且l≠2,m≠2),使得cl、c2、cm成等比数列,若存在,求出l、m的值;若不存在,请说明理由.
,问是否存在正整数l,m(l<m,且l≠2,m≠2),使得cl、c2、cm成等比数列,若存在,求出l、m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220.240),[240,260),[260,280),[280,300)分组的频率分布直方图如图. 
(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为,[220,240),[240,260),[260,280),[280,300)的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数y=f(x)对任意的x都满足f(x+1)=﹣f(x),当﹣1≤x<1时,f(x)=x3 , 若函数g(x)=f(x)﹣loga|x|至少6个零点,则a取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班同学准备参加学校在寒假里组织的“社区服务”、“进敬老院”、“参观工厂”、“民俗调查”、“环保宣传”五个项目的社会实践活动,每天只安排一项活动,并要求在周一至周五内完成.其中“参观工厂”与“环保宣讲”两项活动必须安排在相邻两天,“民俗调查”活动不能安排在周一.则不同安排方法的种数是( )
A.48 B.24 C.36 D.64
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列an}的前n项和为Sn , a1=1,a2=2,且点(Sn , Sn+1)在直线y=tx+1上.
(1)求Sn及an;
(2)若数列{bn}满足bn= ![]() (n≥2),b1=1,数列{bn}的前n项和为Tn , 求证:当n≥2时,Tn<2.
(n≥2),b1=1,数列{bn}的前n项和为Tn , 求证:当n≥2时,Tn<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对任意m∈R,直线mx﹣y+1=0与圆x2+y2=r2(r>0)交于不同的两点A、B,且存在m使| ![]() +
+ ![]() |≥|
|≥| ![]() |(O是坐标原点)成立,那么r的取值范围是( )
|(O是坐标原点)成立,那么r的取值范围是( )
A.0<r≤ ![]()
B.1<r< ![]()
C.1<r≤ ![]()
D.r> ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:关于x的方程ax2+2x+1=0至少有一个负根,q:a≤1,则¬p是¬q的( )
A.充要条件
B.充分不必要条件
C.必要不充分条件
D.不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com