
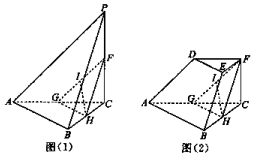
 如图(1),三棱锥P-ABC中,PC⊥平面ABC,F,G,H,分别是PC,AC,BC的中点,I是线段FG上任意一点,PC=AB=2BC,过点F作平行于底面ABC的平面截三棱锥,得到几何体DEF-ABC,如图(2)所示.
如图(1),三棱锥P-ABC中,PC⊥平面ABC,F,G,H,分别是PC,AC,BC的中点,I是线段FG上任意一点,PC=AB=2BC,过点F作平行于底面ABC的平面截三棱锥,得到几何体DEF-ABC,如图(2)所示.分析 (1)利用中位线定理、面面线面平行的判定与性质定理即可证明.
(2)利用余弦定理可得cos∠GHF,根据VC-FGH=VF-CGH,即可得出.
解答 (1)证明:∵F,G,H,分别是PC,AC,BC的中点,∴GH∥AB,FG∥PA.∵GH?平面PAB,FG?平面PAB,
∴GH∥平面PAB,FG∥平面PAB.∵FG∩GH=G,∴平面PAB∥平面FGH.∵HI?平面FGH,∴HI∥平面ABD.
(2)解:由题意可得:HF=$\frac{\sqrt{5}}{2}$,HG=1,GF=$\frac{\sqrt{7}}{2}$.
故cos∠GHF=$\frac{1+\frac{5}{4}-\frac{7}{4}}{2×1×\frac{\sqrt{5}}{2}}$=$\frac{\sqrt{5}}{10}$.故sin∠GHF=$\frac{\sqrt{95}}{10}$,记点C到平面FGH的距离为h,
∵VC-FGH=VF-CGH,
∴$\frac{1}{3}×(\frac{1}{2}×\frac{1}{2}×\frac{\sqrt{3}}{2})$×1=$\frac{1}{3}×$$(\frac{1}{2}×1×\frac{\sqrt{5}}{2}×\frac{\sqrt{95}}{10})$×h,
解得h=$\frac{\sqrt{57}}{19}$.
点评 本题考查了面面线面平行的判定与性质定理、三角形中位线定理、“等体积变形”,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 对此事的态度 | 好评(有利于百姓出行) | 中评(影响不大) | 差评(纯属忽悠) | 不关心 |
| 人数 | 2000 | 4000 | 3000 | 1000 |
| A. | 10 | B. | 8 | C. | 5 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $-\frac{{\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $-\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{14}{13}$ | C. | $\frac{56}{41}$ | D. | $\frac{29}{23}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com