
【题目】如果存在常数a,使得数列{an}满足:若x是数列{an}中的一项,则a﹣x也是数列{an}中的一项,称数列{an}为“兑换数列”,常数a是它的“兑换系数”.
(1)若数列:2,3,6,m(m>6)是“兑换系数”为a的“兑换数列”,求m和a的值;
(2)已知有穷等差数列{bn}的项数是n0(n0≥3),所有项之和是B,求证:数列{bn}是“兑换数列”,并用n0和B表示它的“兑换系数”;
(3)对于一个不少于3项,且各项皆为正整数的递增数列{cn},是否有可能它既是等比数列,又是“兑换数列”?给出你的结论,并说明理由.
【答案】
(1)解:因为2,3,6,m(m>6)是“兑换系数”为a的“兑换数列”
所以a﹣m,a﹣6,a﹣3,a﹣2也是该数列的项,且a﹣m<a﹣6<a﹣3<a﹣2,
故a﹣m=2,a﹣6=3,即a=9,m=7
(2)证明:设数列{bn}的公差为d,
因为数列{bn}是项数为n0项的有穷等差数列
若b1≤b2≤b3≤…≤b ![]() ,则a﹣b1≥a﹣b2≥a﹣b3≥…≥a﹣b
,则a﹣b1≥a﹣b2≥a﹣b3≥…≥a﹣b ![]() ,
,
即对数列{bn}中的任意一项bi(1≤i≤n0),a﹣bi=b1+(n0﹣i)d=b ![]() +1﹣i∈{bn}
+1﹣i∈{bn}
同理可得:b1≥b2≥b3≥…≥b ![]() ,a﹣bi=b1+(n0﹣i)d=b
,a﹣bi=b1+(n0﹣i)d=b ![]() +1﹣i∈{bn}也成立,
+1﹣i∈{bn}也成立,
由“兑换数列”的定义可知,数列{bn}是“兑换数列”;
又因为数列{bn}所有项之和是B,所以B= ![]() =
= ![]() ,即a=
,即a= ![]()
(3)解:假设存在这样的等比数列{cn},设它的公比为q(q>1),
因为数列{cn}为递增数列,所以c1<c2<c3<…<cn,则a﹣c1>a﹣c2>a﹣c3>…>a﹣cn,
又因为数列{cn}为“兑换数列”,则a﹣ci∈{cn},所以a﹣ci是正整数
故数列{cn}必为有穷数列,不妨设项数为n项,则ci+cn+1﹣i=a(1≤i≤n)
①若n=3,则有c1+c3=a,c2= ![]() ,又c22=c1c3,由此得q=1,与q>1矛盾
,又c22=c1c3,由此得q=1,与q>1矛盾
②若n≥4,由c1+cn=c2+cn﹣1,得c1﹣c1q+c1qn﹣1﹣c1qn﹣2=0
即(q﹣1)(1﹣qn﹣2)=0,故q=1,与q>1矛盾;
综合①②得,不存在满足条件的数列{cn}
【解析】(1)根据数列:2,3,6,m(m>6)是“兑换系数”为a的“兑换数列”所以a﹣m,a﹣6,a﹣3,a﹣2也是该数列的项,且a﹣m<a﹣6<a﹣3<a﹣2,由此可求m和a的值;(2)由“兑换数列”的定义证明数列{bn}是“兑换数列”,即证对数列{bn}中的任意一项bi(1≤i≤n0),a﹣bi=b1+(n0﹣i)d=bn0+1﹣i∈{bn},从而可求数列{bn}所有项之和;(3)假设存在这样的等比数列{cn},设它的公比为q(q>1),可知数列{cn}必为有穷数列,不妨设项数为n项,则ci+cn+1﹣i=a(1≤i≤n),再分类讨论,即可得到结论.


科目:高中数学 来源: 题型:
【题目】如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点. 
(1)求证:GH∥平面ADPE;
(2)M是线段PC上一点,且PM= ![]() ,求二面角C﹣EF﹣M的余弦值.
,求二面角C﹣EF﹣M的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+b(a,b∈R),曲线f(x)在x=1处的切线方程为x﹣y﹣1=0.
(Ⅰ)求a,b的值;
(Ⅱ)证明: ![]() ;
;
(Ⅲ)已知满足xlnx=1的常数为k.令函数g(x)=mex+f(x)(其中e是自然对数的底数,e=2.71828…),若x=x0是g(x)的极值点,且g(x)≤0恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且满足acosB=bcosA.
(1)判断△ABC的形状;
(2)求sin(2A+ ![]() )﹣2cos2B的取值范围.
)﹣2cos2B的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知x,y∈R,且 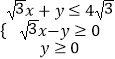 ,则存在θ∈R,使得xcosθ+ysinθ+1=0成立的P(x,y)构成的区域面积为( )
,则存在θ∈R,使得xcosθ+ysinθ+1=0成立的P(x,y)构成的区域面积为( )
A.4 ![]() ﹣
﹣ ![]()
B.4 ![]() ﹣
﹣ ![]()
C.![]()
D.![]() +
+ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为2,则输出的v值为( ) 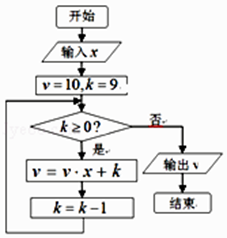
A.9×210﹣2
B.9×210+2
C.9×211+2
D.9×211﹣2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣x2+2a+b(x∈R)的图象在x=0处的切线为y=bx.(e为自然对数的底数).
(Ⅰ)求a,b的值;
(Ⅱ)若k∈Z,且f(x)+ ![]() (3x2﹣5x﹣2k)≥0对任意x∈R恒成立,求k的最大值.
(3x2﹣5x﹣2k)≥0对任意x∈R恒成立,求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1 , F2为椭圆E的左右焦点,点P(1, ![]() )为其上一点,且有|PF1|+|PF2|=4
)为其上一点,且有|PF1|+|PF2|=4
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)过F1的直线l1与椭圆E交于A,B两点,过F2与l1平行的直线l2与椭圆E交于C,D两点,求四边形ABCD的面积SABCD的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分8分)某班50名学生在一次数学测试中,成绩全部介于50与100之间,将测试结果按如下方式分成五组:第一组[50,60),第二组[60,70),…,第五组[90,100].如图所示是按上述分组方法得到的频率分布直方图.

(Ⅰ)若成绩大于或等于60且小于80,认为合格,求该班在这次数学测试中成绩合格的人数;
(Ⅱ)从测试成绩在[50,60)∪[90,100]内的所有学生中随机抽取两名同学,设其测试成绩分别为m、n,求事件“|m﹣n|>10”概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com