
【题目】电视传媒公司为了解某地区观众对某类休育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
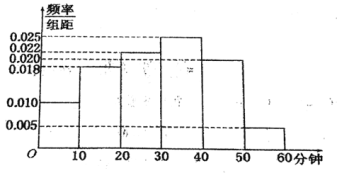
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
(1)根据已知条件完成下面的![]() 列联表,并据此资料判断是否有
列联表,并据此资料判断是否有![]() 的把握认为“体育迷”与性别有关?
的把握认为“体育迷”与性别有关?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | |||
合计 |
(2)将日均收看读体育节目不低于50分钟的观众称为“超级体育迷”,已知“超级体育迷”中有2名女性,若从“超级体育迷”中任意选取2人,求至少有1名女性观众的概率.
附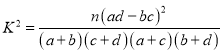 .
.
| 0.05 | 0.01 |
| 3.841 | 6.635 |
【答案】(1)填表见解析;没有![]() 的把握认为“体育迷”与性别有关(2)
的把握认为“体育迷”与性别有关(2)![]()
【解析】
(1)根据频率分布直方图,在抽取的100人中,其中女性有55名,“体育迷”有25人,其中有10名女性完成![]() 列联表,.然后计算
列联表,.然后计算![]() 值,与
值,与![]() 表对照下结论.
表对照下结论.
(2)由频率分布直方图可知,“超级体育迷”为5人,其中3名男性,2名女性,根据古典概型,先列举一切可能结果所组成的基本事件数,再找出“任选2人中,至少有1人是女性”的基本事件数,代入公式求解.
(1)由频率分布直方图可知,在抽取的100人中,“体育迷”有25人,从而完成![]() 列联表如下:
列联表如下:
非体育迷 | 体育迷 | 合计 | |
男 | 30 | 15 | 45 |
女 | 45 | 10 | 55 |
合计 | 75 | 25 | 100 |
将![]() 列联表中的数据代入公式计算,得
列联表中的数据代入公式计算,得
![]() .
.
因为![]() ,
,
所以我们没有![]() 的把握认为“体育迷”与性别有关.
的把握认为“体育迷”与性别有关.
(2)由频率分布直方图可知,“超级体育迷”为5人,其中![]() 表示男性,
表示男性,![]() ,
,![]() 表示女性,
表示女性,![]() ,
,
从而一切可能结果所组成的基本事件为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() , 由10个基本事件组成,而且这些基本事件的出现是等可能的.
, 由10个基本事件组成,而且这些基本事件的出现是等可能的.
用![]() 表示“任选2人中,至少有1人是女性”这一事件,则
表示“任选2人中,至少有1人是女性”这一事件,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,由7个基本事件组成,
,由7个基本事件组成,
所以![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知集合A={x|2a+1≤x≤3a-5},B={x|x<-1,或x>16},分别根据下列条件求实数a的取值范围.
(1)A∩B=![]() ;(2)A(A∩B).
;(2)A(A∩B).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,有一边长为2的正方形ABCD,E是边AD的中点,将![]() 沿着直线BE折起至
沿着直线BE折起至![]() 位置(如图2),此时恰好
位置(如图2),此时恰好![]() ,点
,点![]() 在底面上的射影为O.
在底面上的射影为O.


(1)求证:![]() ;
;
(2)求直线![]() 与平面BCDE所成角的正弦值.
与平面BCDE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用清水漂洗衣服上残留的洗衣液,对用一定量的清水漂洗一次的效果作如下假定:用1个单位量的水可洗掉衣服上残留洗衣液质量的一般,用水越多漂洗效果越好,但总还有洗衣液残留在衣服上.设用![]() 单位量的清水漂洗一次后,衣服上残留的洗衣液质量与本次漂洗前残留的洗衣液质量之比为函数
单位量的清水漂洗一次后,衣服上残留的洗衣液质量与本次漂洗前残留的洗衣液质量之比为函数![]() ,其中
,其中![]() .
.
(1)试规定![]() 的值,并解释其实际意义;
的值,并解释其实际意义;
(2)根据假定写出函数![]() 应该满足的条件和具有的性质,并写出满足假定的一个指数函数;
应该满足的条件和具有的性质,并写出满足假定的一个指数函数;
(3)设函数![]() .现有
.现有![]() (
(![]() )单位量的清水,可供漂洗一次,也可以把水平均分成2份后先后漂洗两次,试确定哪种方式漂洗效果更好?并说明理由.
)单位量的清水,可供漂洗一次,也可以把水平均分成2份后先后漂洗两次,试确定哪种方式漂洗效果更好?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
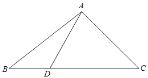
【题目】如图所示,在△ABC中,D是BC边上的一点,且AB=14,BD=6,∠ADC=![]() ,
,![]() .
.
(Ⅰ)求sin∠DAC;
(Ⅱ)求AD的长和△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日是第二十七届“世界水日”,
日是第二十七届“世界水日”,![]() 月
月![]() 日是第三十二届“中国水周”.我国纪念
日是第三十二届“中国水周”.我国纪念![]() 年“世界水日”和“中国水周”活动的宣传主题为“坚持节水优先,强化水资源管理”.某中学课题小组抽取
年“世界水日”和“中国水周”活动的宣传主题为“坚持节水优先,强化水资源管理”.某中学课题小组抽取![]() 、
、![]() 两个小区各
两个小区各![]() 户家庭,记录他们
户家庭,记录他们![]() 月份的用水量(单位:
月份的用水量(单位:![]() )如下表:
)如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据两组数据完成下面的茎叶图,从茎叶图看,哪个小区居民节水意识更好?
|
| |
| ||
| ||
| ||
|
(2)从用水量不少于![]() 的家庭中,
的家庭中,![]() 、
、![]() 两个小区各随机抽取一户,求
两个小区各随机抽取一户,求![]() 小区家庭的用水量低于
小区家庭的用水量低于![]() 小区的概率.
小区的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com