
【题目】已知抛物线![]() 的方程为
的方程为![]() ,其焦点为
,其焦点为![]() ,
,![]() 为过焦点
为过焦点![]() 的抛物线
的抛物线![]() 的弦,过
的弦,过![]() 分别作抛物线的切线
分别作抛物线的切线![]() ,
,![]() ,设
,设![]() ,
,![]() 相交于点
相交于点![]() .
.
(1)求![]() 的值;
的值;
(2)如果圆![]() 的方程为
的方程为![]() ,且点
,且点![]() 在圆
在圆![]() 内部,设直线
内部,设直线![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的最小值.
的最小值.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)设点![]() 分别为曲线
分别为曲线![]() 与曲线
与曲线![]() 上的任意一点,求
上的任意一点,求![]() 的最大值;
的最大值;
(2)设直线![]() (
(![]() 为参数)与曲线
为参数)与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的焦点分别为
的焦点分别为![]() ,
,![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() ,且经过点
,且经过点![]() ,经过
,经过![]() ,
,![]() 作平行直线
作平行直线![]() ,
,![]() ,交椭圆
,交椭圆![]() 于两点
于两点![]() ,
,![]() 和两点
和两点![]() ,
,![]() .
.
(1)求![]() 的方程;
的方程;
(2)求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为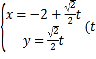 为参数
为参数![]() ,直线
,直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点.
两点.
(1)若点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值;
的值;
(2)求曲线![]() 的内接矩形周长的最大值.
的内接矩形周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义向量的外积:![]() 叫做向量
叫做向量![]() 与
与![]() 的外积,它是一个向量,满足下列两个条件:
的外积,它是一个向量,满足下列两个条件:
(1)![]() ,
,![]() ,且
,且![]() ,
,![]() 和
和![]() 构成右手系(即三个向量两两垂直,且三个向量的方向依次与拇指、食指、中指的指向一致);
构成右手系(即三个向量两两垂直,且三个向量的方向依次与拇指、食指、中指的指向一致);
(2)![]() 的模
的模![]() (
(![]() 表示向量
表示向量![]() 、
、![]() 的夹角);
的夹角);
如图,在正方体![]() ,有以下四个结论:
,有以下四个结论:
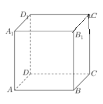
①![]() 与
与![]() 方向相反;
方向相反;
②![]() ;
;
③![]() 与正方体表面积的数值相等;
与正方体表面积的数值相等;
④![]() 与正方体体积的数值相等.
与正方体体积的数值相等.
这四个结论中,正确的结论有( )个
A.4B.3C.2D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017高考新课标Ⅲ,理19)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.

(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D–AE–C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() =
=![]() .
.
(1)若不等式![]() 的解集为
的解集为![]() ,求不等式
,求不等式![]() 的解集;
的解集;
(2)若对于任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)已知![]() ,若方程
,若方程![]() 在
在![]() 有解,求实数
有解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com