(1)解:∵a
1=1,na
n+1=2(a
1+a
2+…+a
n),
∴a
2=2a
1=2,
2a
3=2(a
1+a
2)=6,a
3=3,
3a
4=2(a
1+a
2+a
3)=12,a
4=4;(3分)
(2)解:na
n+1=2(a
1+a
2++a
n)①
(n-1)a
n=2(a
1+a
2+…+a
n-1)②
①-②得na
n+1-(n-1)a
n=2a
n,
即:na
n+1=(n+1)a
n,
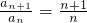
(6分)
所以
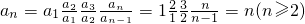
所以a
n=n(n∈N
*);(8分)
(3)证明:①由(2)得:
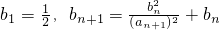
>b
n>b
n-1>…>b
1>0,
所以数列{b
n}是正项单调递增数列,(10分)
当n≥1,
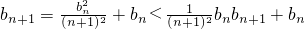
,
所以
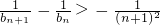
,(12分)
②1°当n=1时,
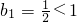
显然成立.
2°当n≥2时,
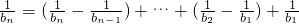
>-
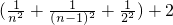
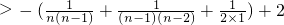
=
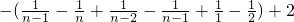
=
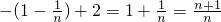
,所以
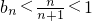
,
综上可知,b
n<1成立.(14分)
分析:(1)由数列{a
n}中,a
1=1,na
n+1=2(a
1+a
2+…+a
n),分别令n=1,2,3,能求出a
2,a
3,a
4.
(2)由na
n+1=2(a
1+a
2+…+a
n),得(n-1)a
n=2(a
1+a
2++a
n-1),二者相减得到na
n+1=(n+1)a
n,由此能求出a
n.
(3)①由(2)得:
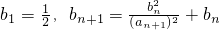
>b
n>b
n-1>…>b
1>0,所以数列{b
n}是正项单调递增数列,由此能够证明
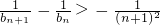
.
②当n=1时,
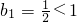
显然成立.当n≥2时,
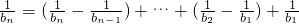
>
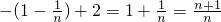
,所以
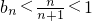
,由此能够证明b
n<1成立.
点评:本题考查数列的通项公式的求法,考查不等式的证明.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意迭代法和放缩法的灵活运用.

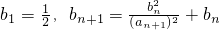 ,证明:①(
,证明:①(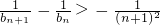 ; ②bn<1.
; ②bn<1.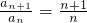 (6分)
(6分)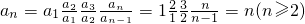
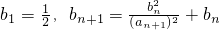 >bn>bn-1>…>b1>0,
>bn>bn-1>…>b1>0,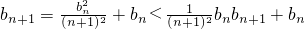 ,
,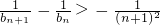 ,(12分)
,(12分)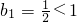 显然成立.
显然成立.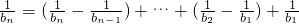
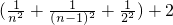
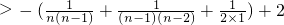
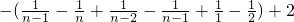
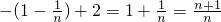 ,所以
,所以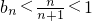 ,
,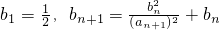 >bn>bn-1>…>b1>0,所以数列{bn}是正项单调递增数列,由此能够证明
>bn>bn-1>…>b1>0,所以数列{bn}是正项单调递增数列,由此能够证明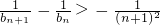 .
.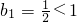 显然成立.当n≥2时,
显然成立.当n≥2时,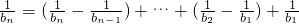 >
>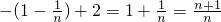 ,所以
,所以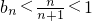 ,由此能够证明bn<1成立.
,由此能够证明bn<1成立.

 阅读快车系列答案
阅读快车系列答案