
【题目】已知函数![]() .
.
(Ⅰ)若过点![]() 恰有两条直线与曲线
恰有两条直线与曲线![]() 相切,求
相切,求![]() 的值;
的值;
(Ⅱ)用![]() 表示
表示![]() 中的最小值,设函数
中的最小值,设函数![]() ,若
,若![]() 恰有三个零点,求实数
恰有三个零点,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)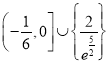 .
.
【解析】试题分析:(Ⅰ)求导,利用导数求得![]() 的过点
的过点![]() 的切线方程,构造辅助函数,利用导数与函数单调性的关系,分类讨论即可得a的值;
的切线方程,构造辅助函数,利用导数与函数单调性的关系,分类讨论即可得a的值;
(Ⅱ)根据函数的定义求![]() ,根据函数的单调性及零点的判断,采用分类讨论法,求得函数
,根据函数的单调性及零点的判断,采用分类讨论法,求得函数![]() 零点的个数,即可求得
零点的个数,即可求得![]() 恰有三个零点,求实数
恰有三个零点,求实数![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ)∵![]() ,∴
,∴![]() ,
,
设切点为![]() ,则该点处的切线方程为
,则该点处的切线方程为![]() ,
,
又∵切线过点![]() ,∴
,∴![]() ,
,
整理得, ![]() ,(*)
,(*)
依题设,方程(*)恰有两个不同的解,
令![]() ,则
,则![]() ,
,
解![]() 得
得![]() ,
,
①当![]() 时,
时, ![]() 恒成立,
恒成立, ![]() 单调递增,至多只有一个零点,不合题设;
单调递增,至多只有一个零点,不合题设;
②当![]() 时,则
时,则![]() 为
为![]() 的极值点,若
的极值点,若![]() 恰有两个不同的解,
恰有两个不同的解,
则![]() 或
或![]() ,又∵
,又∵![]() ,
,
![]() ,∴
,∴![]() 或
或![]() .
.
令![]() ,则
,则![]() ,
,
解![]() 得
得![]() ,∴
,∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
又∵![]() , ∴当
, ∴当![]() 且
且![]() 时,
时, ![]() 无解. ∴
无解. ∴![]() .
.
(Ⅱ)∵![]() ,
,
∴当![]() 时,解
时,解![]() 得
得![]() .
.
由(Ⅰ)知, ![]() ,
,
当![]() 时,
时, ![]() ;当
;当![]() 或
或![]() 时,
时, ![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
∴当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() .
.
∵![]() , ∴
, ∴![]() ,
,
∴当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递减,
上单调递减,
∵![]() ,∴
,∴![]() .
.
∴当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
此时![]() 恰有三个零点.
恰有三个零点.
当![]() 时,
时, ![]() ,解
,解![]() 得
得![]() ,
,
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
∴![]() ,当
,当![]() 时,
时, ![]() ,此时不合题意;
,此时不合题意;
当![]() 时,
时, ![]() 恰有一个零点
恰有一个零点![]() ,此时符合题意;
,此时符合题意;
当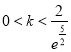 时,
时, ![]() ,
, ![]() ,
,
又∵![]() ,当
,当![]() 时,
时, ![]() .
.
∴![]() 在
在![]() 上有两个零点,此时
上有两个零点,此时![]() 在
在![]() 上有4个零点,不合题设.
上有4个零点,不合题设.
综上, ![]() 的取值范围是
的取值范围是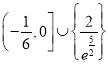 .
.
点晴:本题考查函数导数与单调性.确定零点的个数问题:可利用数形结合的办法判断交点个数,如果函数较为复杂,可结合导数知识确定极值点和单调区间从而确定其大致图象.方程的有解问题就是判断是否存在零点的问题,可参变分离,转化为求函数的值域问题处理. 恒成立问题以及可转化为恒成立问题的问题,往往可利用参变分离的方法,转化为求函数最值处理.也可构造新函数然后利用导数来求解.注意利用数形结合的数学思想方法.


科目:高中数学 来源: 题型:
【题目】如图所示,我艇在A处发现一走私船在方位角45°且距离为12海里的B处正以每小时10海里的速度向方位角105°的方向逃窜,我艇立即以14海里/小时的速度追击,求我艇追上走私船所需要的最短时间. 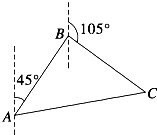
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双流中学2016年高中毕业的大一学生假期参加社会实践活动,为提高某套丛书的销量,准备举办一场展销会,据市场调查,当每套丛书售价定为![]() 元时,销售量可达到
元时,销售量可达到![]() 万套,现出版社为配合该书商的活动,决定进行价格改革,将每套丛书的供货价格分成固定价格和浮动价格两部分,其中固定价格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为10,假设不计其他成本,即销售每套丛书的利润=售价
万套,现出版社为配合该书商的活动,决定进行价格改革,将每套丛书的供货价格分成固定价格和浮动价格两部分,其中固定价格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为10,假设不计其他成本,即销售每套丛书的利润=售价![]() 供货价格.问:
供货价格.问:
(1)每套丛书售价定为100元时,书商所获得的总利润是多少万元?
(2)每套丛书售价定为多少元时,单套丛书的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列 ![]() ,﹣
,﹣ ![]() ,
, ![]() ,﹣
,﹣ ![]() ,…的一个通项公式为( )
,…的一个通项公式为( )
A.an=(﹣1)n ![]()
B.an=(﹣1)n ![]()
C.an=(﹣1)n+1 ![]()
D.an=(﹣1)n+1 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知由甲、乙两位男生和丙、丁两位女生组成的四人冲关小组,参加由安徽卫视推出的大型户外竞技类活动《男生女生向前冲》.活动共有四关,若四关都闯过,则闯关成功,否则落水失败.设男生闯过一至四关的概率依次是![]() ,女生闯过一至四关的概率依次是
,女生闯过一至四关的概率依次是![]() .
.
(Ⅰ)求男生甲闯关失败的概率;
(Ⅱ)设![]() 表示四人冲关小组闯关成功的人数,求随机变量
表示四人冲关小组闯关成功的人数,求随机变量![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且满足 ![]() acosC﹣csinA=0.
acosC﹣csinA=0.
(1)求角C的大小;
(2)已知b=4,△ABC的面积为6 ![]() ,求边长c的值.
,求边长c的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com