
【题目】在平面直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程为![]() (1+cos2θ)=8sinθ.
(1+cos2θ)=8sinθ.
(1)求曲线C的普通方程;
(2)直线l的参数方程为![]() ,t为参数直线
,t为参数直线![]() 与y轴交于点F与曲线C的交点为A,B,当|FA||FB|取最小值时,求直线
与y轴交于点F与曲线C的交点为A,B,当|FA||FB|取最小值时,求直线![]() 的直角坐标方程.
的直角坐标方程.
【答案】(1)x2=4y;(2)y=1
【解析】
(1)根据x=ρcosθ,y=ρsinθ将极坐标方程化为普通方程,(2)将直线参数方程代入抛物线方程,利用韦达定理以及参数几何意义求|FA||FB|,最后根据三角函数有界性确定最值,解得结果.
(1)由题意得ρ(1+cos2θ)=8sinθ,得2ρcos2θ=8sinθ,得ρ2cos2θ=4ρsinθ,
∵x=ρcosθ,y=ρsinθ,∴x2=4y,即曲线C的普通方程为x2=4y.
(2)由题意可知,直线![]() 与y轴交于点F(0,1)即为抛物线C的焦点,
与y轴交于点F(0,1)即为抛物线C的焦点,
令|FA|=|t1|,|FB|=|t2|,将直线![]() 的参数方程
的参数方程![]() 代入C的普通方程x2=4y中,
代入C的普通方程x2=4y中,
整理得t2cos2α-4tsinα-4=0,
由题意得cosα≠0,根据韦达定理得:t1+t2=![]() ,t1t2=
,t1t2=![]() ,
,
∴|FA||FB|=|t1||t2|=|t1t2|=![]() ≥4,(当且仅当cos2α=1时,等号成立),
≥4,(当且仅当cos2α=1时,等号成立),
∴当|FA||FB|取得最小值时,直线![]() 的直角坐标方程为y=1.
的直角坐标方程为y=1.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的坐标为
的坐标为![]() ,若点
,若点![]() 是曲线
是曲线![]() 截直线
截直线![]() 所得线段的中点,求
所得线段的中点,求![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,将曲线
,将曲线![]() 向左平移
向左平移![]() 个单位长度得到曲线
个单位长度得到曲线![]() .
.
(1)求曲线![]() 的参数方程;
的参数方程;
(2)已知![]() 为曲线
为曲线![]() 上的动点,
上的动点, ![]() 两点的极坐标分别为
两点的极坐标分别为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国仓储指数是反映仓储行业经营和国内市场主要商品供求状况与变化趋势的已套指数体系.如图所示的折线图是2017年和2018年的中国仓储指数走势情况.根据该折线图,下列结论中不正确的是( )
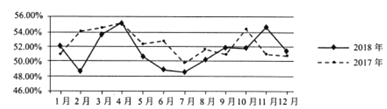
A. 2018年1月至4月的仓储指数比2017年同期波动性更大
B. 这两年的最大仓储指数都出现在4月份
C. 2018年全年仓储指数平均值明显低于2017年
D. 2018年各仓储指数的中位数与2017年各仓储指数中位数差异明显
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底而ABCD是菱形,且PA=AD=2,∠PAD=∠BAD=120°,E,F分别为PD,BD的中点,且![]() .
.
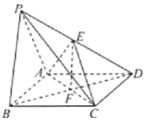
(1)求证:平面PAD⊥平面ABCD;
(2)求锐二面角E-AC-D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了变废为宝,节约资源,新上了一个从生活垃圾中提炼生物柴油的项目.经测算该项目月处理成本![]() (元)与月处理量
(元)与月处理量![]() (吨)之间的函数关系可以近似地表示为:
(吨)之间的函数关系可以近似地表示为:
 ,且每处理一吨生活垃圾,可得到能利用的生物柴油价值为200元,若该项目不获利,政府将给予补贴.
,且每处理一吨生活垃圾,可得到能利用的生物柴油价值为200元,若该项目不获利,政府将给予补贴.
(1)当![]() 时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损?
时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损?
(2)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C过点A(2,6),且与直线l1: x+y-10=0相切于点B(6,4).
(1)求圆C的方程;
(2)过点P(6,24)的直线l2与圆C交于M,N两点,若△CMN为直角三角形,求直线l2的斜率;
(3)在直线l3: y=x-2上是否存在一点Q,过点Q向圆C引两切线,切点为E,F, 使△QEF为正三角形,若存在,求出点Q的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一个四位数的各位数字相加和为10,则称该数为“完美四位数”,如数字“2017”.试问用数字0,1,2,3,4,5,6,7组成的无重复数字且大于2017的“完美四位数”有( )个.
A. 71B. 66C. 59D. 53
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨.销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元.该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨.
(1)列出甲、乙两种产品满足的关系式,并画出相应的平面区域;
(2)在一个生产周期内该企业生产甲、乙两种产品各多少吨时可获得利润最大,最大利润是多少?
(用线性规划求解要画出规范的图形及具体的解答过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com