
【题目】2020年我国全面建成小康社会,其中小康生活的住房标准是城镇人均住房建筑面积30平方米. 下表为2007年—2016年中,我区城镇和农村人均住房建筑面积统计数据. 单位:平方米.
2007年 | 2008年 | 2009年 | 2010年 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 | |
城镇 | 18.66 | 20.25 | 22.79 | 25 | 27.1 | 28.3 | 31.6 | 32.9 | 34.6 | 36.6 |
农村 | 23.3 | 24.8 | 26.5 | 27.9 | 30.7 | 32.4 | 34.1 | 37.1 | 41.4 | 45.8 |
(1)现从上述表格中随机抽取一年数据,试估计该年城镇人均住房建筑面积达到小康生活住房标准的概率;
(2)现从上述表格中随机抽取连续两年数据,求这两年中城镇人均住房建筑面积增长不少于2平方米的概率;
(3)将城镇和农村的人均住房建筑面积经四舍五入取整后作为样本数据.记2012—2016年中城镇人均住房面积的方差为![]() ,农村人均住房面积的方差为
,农村人均住房面积的方差为![]() ,判断
,判断![]() 与
与![]() 的大小.(只需写出结论).
的大小.(只需写出结论).
(注:方差![]() ,其中
,其中![]() 为
为 ![]()
![]() ,……
,…… ![]() 的平均数)
的平均数)
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
![]()
【解析】
(1)利用古典概型的概率得该年城镇人均住房建筑面积达到小康生活住房标准的概率为![]() ;(2)先求出总的次数,再计算两年中城镇人均住房建筑面积增长不少于2平方米的次数,再利用古典概型求解;(3)先求出平均数,再求方差即得
;(2)先求出总的次数,再计算两年中城镇人均住房建筑面积增长不少于2平方米的次数,再利用古典概型求解;(3)先求出平均数,再求方差即得![]() 与
与![]() 的大小.
的大小.
(1)记事件![]() 为该年城镇人均住房建筑面积达到小康生活住房标准
为该年城镇人均住房建筑面积达到小康生活住房标准![]()
所以该年城镇人均住房建筑面积达到小康生活住房标准的概率为![]() .
.
(2)随机抽取连续两年数据共9次,两年中城镇人均住房建筑面积增长不少于2平方米:共5次。设“两年中城镇人均住房建筑面积增长不少于2平方米”为事件![]() ,因此
,因此![]() .
.
(3)由题得
2012年 | 2013年 | 2014年 | 2015年 | 2016年 | |
城镇 | 28 | 32 | 33 | 35 | 37 |
农村 | 32 | 34 | 37 | 41 | 46 |
由题得城镇住房面积的平均数为33,
所以2012—2016年中城镇人均住房面积的方差为
![]() =
=![]()
![]() ,
,
由题得城镇住房面积的平均数为36,
所以2012—2016年中城镇人均住房面积的方差为
![]() =
=![]()
![]() ,
,
所以![]()
![]() .
.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 作垂直于
作垂直于![]() 轴的直线与抛物线交于
轴的直线与抛物线交于![]() ,
,![]() 两点,且以线段
两点,且以线段![]() 为直径的圆过点
为直径的圆过点![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 为曲线
为曲线![]() :
:![]() 上的动点,求
上的动点,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(选做题)
A.[选修4-2:矩阵与变换](本小题满分10分)
已知m,n∈R,向量![]() 是矩阵
是矩阵![]() 的属于特征值3的一个特征向量,求矩阵M及另一个特征值.
的属于特征值3的一个特征向量,求矩阵M及另一个特征值.
B.[选修4-4:坐标系与参数方程](本小题满分10分)
在平面直角坐标系xOy中,已知直线![]() 的参数方程为
的参数方程为![]() ( t为参数),椭圆C的参数方程为
( t为参数),椭圆C的参数方程为![]() .设直线
.设直线![]() 与椭圆C交于A,B两点,求线段AB的长.
与椭圆C交于A,B两点,求线段AB的长.
C.[选修4-5:不等式选讲](本小题满分10分)
已知x,y,z均是正实数,且![]() 求证:
求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,满足(2b﹣c)cosA=acosC.
(1)求角A;
(2)若![]() ,b+c=5,求△ABC的面积.
,b+c=5,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程,并说明它为何种曲线;
的直角坐标方程,并说明它为何种曲线;
(Ⅱ)设点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为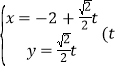 为参数
为参数![]() ,直线
,直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点.
两点.
(1)若点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值;
的值;
(2)求曲线![]() 的内接矩形周长的最大值.
的内接矩形周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设椭圆![]() :
: ![]() ,长轴的右端点与抛物线
,长轴的右端点与抛物线![]() :
: ![]() 的焦点
的焦点![]() 重合,且椭圆
重合,且椭圆![]() 的离心率是
的离心率是![]() .
.
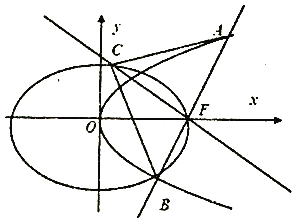
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过![]() 作直线
作直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
, ![]() 两点,过
两点,过![]() 且与直线
且与直线![]() 垂直的直线交椭圆
垂直的直线交椭圆![]() 于另一点
于另一点![]() ,求
,求![]() 面积的最小值,以及取到最小值时直线
面积的最小值,以及取到最小值时直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com