
【题目】已知定义域为![]() 的函数
的函数![]() 是奇函数
是奇函数
(Ⅰ)求![]() 值;
值;
(Ⅱ)判断并证明该函数在定义域![]() 上的单调性;
上的单调性;
(Ⅲ)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅳ)设关于![]() 的函数
的函数![]() 有零点,求实数
有零点,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ) ![]() ;(Ⅱ)答案见解析;(Ⅲ)
;(Ⅱ)答案见解析;(Ⅲ) ![]() (Ⅳ)
(Ⅳ)![]() .
.
【解析】试题分析:(1)根据奇函数性质得![]() ,解得
,解得![]() 值;(2)根据单调性定义,作差通分,根据指数函数单调性确定因子符号,最后根据差的符号确定单调性(3)根据奇偶性以及单调性将不等式化为一元二次不等式恒成立问题,利用判别式求实数
值;(2)根据单调性定义,作差通分,根据指数函数单调性确定因子符号,最后根据差的符号确定单调性(3)根据奇偶性以及单调性将不等式化为一元二次不等式恒成立问题,利用判别式求实数![]() 的取值范围;(4)根据奇偶性以及单调性将方程转化为一元二次方程有解问题,根据二次函数图像与性质求值域,即得实数
的取值范围;(4)根据奇偶性以及单调性将方程转化为一元二次方程有解问题,根据二次函数图像与性质求值域,即得实数![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ)由题设,需![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
经验证, ![]() 为奇函数,∴
为奇函数,∴![]() .
.
(Ⅱ)减函数
证明:任取![]() ,
, ![]() ,且
,且![]() ,则
,则![]() ,
,
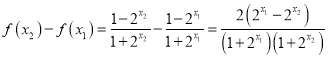
∵![]()
∴![]()
∴![]() ,
, ![]() ;
;
∴![]() ,即
,即![]()
∴该函数在定义域![]() 上是减函数.
上是减函数.
(Ⅲ)由![]() 得
得![]() ,
,
∵![]() 是奇函数,∴
是奇函数,∴![]() ,
,
由(Ⅱ)知, ![]() 是减函数
是减函数
∴原问题转化为![]() ,即
,即![]() 对任意
对任意![]() 恒成立,
恒成立,
∴![]() ,得
,得![]() 即为所求.
即为所求.
(Ⅳ)原函数零点的问题等价于方程![]()
由(Ⅱ)知, ![]() ,即方程
,即方程![]() 有解
有解
∵![]() ,
,
∴当![]() 时函数存在零点.
时函数存在零点.
点睛:利用函数性质解不等式:首先根据函数的性质把不等式转化为![]() 的形式,然后根据函数的单调性去掉“
的形式,然后根据函数的单调性去掉“![]() ”,转化为具体的不等式(组),此时要注意
”,转化为具体的不等式(组),此时要注意![]() 与
与![]() 的取值应在外层函数的定义域内.
的取值应在外层函数的定义域内.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
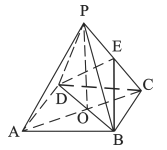
【题目】如图,正四棱锥![]() 中,
中, ![]() 是正方形,
是正方形, ![]() 是正方形的中心,
是正方形的中心, ![]() 底面
底面![]() ,
, ![]() 是
是![]() 的中点.
的中点.
(I)证明: ![]() 平面
平面![]() ;
;
(II)证明:平面![]() 平面
平面![]() ;
;
(III)已知: ![]() ,求点
,求点![]() 到面
到面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大西洋鲑鱼每年都要逆流而上,游回产地产卵,研究鲑鱼的科学家发现鲑鱼的游速![]() (单位:
(单位: ![]() )与其耗氧量单位数
)与其耗氧量单位数![]() 之间的关系可以表示为函数
之间的关系可以表示为函数![]() ,其中
,其中![]() 为常数,已知一条鲑鱼在静止时的耗氧量为100个单位;而当它的游速为
为常数,已知一条鲑鱼在静止时的耗氧量为100个单位;而当它的游速为![]() 时,其耗氧量为2700个单位.
时,其耗氧量为2700个单位.
(1)求出游速![]() 与其耗氧量单位数
与其耗氧量单位数![]() 之间的函数解析式;
之间的函数解析式;
(2)求当一条鲑鱼的游速不高于![]() 时,其耗氧量至多需要多少个单位?
时,其耗氧量至多需要多少个单位?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱柱ABC﹣A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2 ![]() ,D是AA1的中点,BD与AB1交于点O,且CO⊥平面ABB1A1 .
,D是AA1的中点,BD与AB1交于点O,且CO⊥平面ABB1A1 . 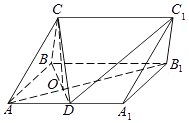
(1)证明:CD⊥AB1;
(2)若OC=OA,求直线CD与平面ABC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)满足:对于s,t∈[0,+∞),都有f(s)≥0,f(t)≥0,且f(s)+f(t)≤f(s+t),则称函数f (x)为“T函数”.
(I)试判断函数f1(x)=x2与f2(x)=lg(x+1)是否是“T函数”,并说明理由;
(Ⅱ)设f (x)为“T函数”,且存在x0∈[0,+∞),使f(f(x0))=x0.求证:f (x0) =x0;
(Ⅲ)试写出一个“T函数”f(x),满足f(1)=1,且使集合{y|y=f(x),0≤x≤1)中元素的个数最少.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F1 , F2分别是C: ![]() +
+ ![]() =1(a>b>0)的左,右焦点,M是C上一点且MF2与x轴垂直,直线MF1与C的另一个交点为N.
=1(a>b>0)的左,右焦点,M是C上一点且MF2与x轴垂直,直线MF1与C的另一个交点为N.
(1)若直线MN的斜率为 ![]() ,求C的离心率;
,求C的离心率;
(2)若直线MN在y轴上的截距为2,且|MN|=5|F1N|,求a,b.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:
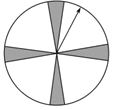
甲商场:顾客转动如图所示圆盘,当指针指向阴影部分(图中四个阴影部分均为扇形,且每个扇形圆心角均为![]() ,边界忽略不计)即为中奖.
,边界忽略不计)即为中奖.
乙商场:从装有3个白球3个红球的盒子中一次性摸出2个球(球除颜色外不加区分),如果摸到的是2个红球,即为中奖.问:购买该商品的顾客在哪家商场中奖的可能性大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com