
【题目】网上购物逐步走进大学生活,某大学学生宿舍4人积极参加网购,大家约定:每个人通过掷一枚质地均匀的骰子决定自己去哪家购物,掷出点数为5或6的人去淘宝网购物,掷出点数小于5的人去京东商城购物,且参加者必须从淘宝网和京东商城选择一家购物.
(1)求这4个人中恰有1人去淘宝网购物的概率;
(2)用![]() ,
,![]() 分别表示这4个人中去淘宝网和京东商城购物的人数,记
分别表示这4个人中去淘宝网和京东商城购物的人数,记![]() ,求随机变量
,求随机变量![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
【答案】(1)![]() ;(2)分布列详见解析,
;(2)分布列详见解析,![]() .
.
【解析】
试题本题主要考查概率、离散型随机变量的分布列和数学期望等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,先求出每个人去淘宝网购物的概率![]() ,去京东商城购物的概率
,去京东商城购物的概率![]() ,再利用二项分布计算恰有1人去淘宝购物的概率;第二问,先写出X的所有可能取值,再利用二项分布分布求出概率,列出分布列,再利用
,再利用二项分布计算恰有1人去淘宝购物的概率;第二问,先写出X的所有可能取值,再利用二项分布分布求出概率,列出分布列,再利用![]() 求出随机变量X的数学期望.
求出随机变量X的数学期望.
试题解析:依题意,这4个人中,每个人去淘宝网购物的概率为![]() ,去京东商城购物的概率为
,去京东商城购物的概率为![]() .设“这4个人中恰有i人去淘宝网购物”为事件
.设“这4个人中恰有i人去淘宝网购物”为事件![]() ,则
,则![]() .
.
(Ⅰ)这4个人中恰有1人去淘宝网购物的概率![]() .
.
(II)易知![]() 的所有可能取值为
的所有可能取值为![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
所以![]() 的分布列是
的分布列是
| 0 | 3 | 4 |
P |
|
|
|
随机变量ξ的数学期望![]() .
.


科目:高中数学 来源: 题型:
【题目】小明跟父母、爷爷奶奶一同参加《中国诗词大会》的现场录制,5人坐成一排.若小明的父母至少有一人与他相邻,则不同坐法的总数为
A. 60 B. 72 C. 84 D. 96
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 过点
过点![]() ,直线
,直线![]() 过点
过点![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
, ![]() 两点.点
两点.点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,连接
,连接![]() .
.

(1)求抛物线线![]() 的标准方程;
的标准方程;
(2)问直线![]() 是否过定点?若是,求出定点坐标;若不是,请说明理由.
是否过定点?若是,求出定点坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了贯彻落实中央省市关于新型冠状病毒肺炎疫情防控工作要求,积极应对新型冠状病毒疫情,切实做好2020年春季开学工作,保障校园安全稳定,普及防控知识,确保师生生命安全和身体健康.某校开学前,组织高三年级800名学生参加了“疫情防控”网络知识竞赛(满分150分).已知这800名学生的成绩均不低于90分,将这800名学生的成绩分组如下:第一组![]() ,第二组
,第二组![]() ,第三组
,第三组![]() ,第四组
,第四组![]() ,第五组
,第五组![]() ,第六组
,第六组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(1)求![]() 的值并估计这800名学生的平均成绩(同一组中的数据用该组区间的中点值代表);
的值并估计这800名学生的平均成绩(同一组中的数据用该组区间的中点值代表);
(2)该校“群防群控”督查组为更好地督促高三学生的“个人防控”,准备从这800名学生中取2名学生参与督查工作,其取办法是:先在第二组第五组第六组中用分层抽样的方法抽取6名学生,再从这6名学生中随机抽取2名学生.记这2名学生的竞赛成绩分别为![]()
![]() .求事件
.求事件![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() .
.
⑴ 求证:数列![]() 为等差数列;
为等差数列;
⑵ 设![]() ,
, ![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,若当
,若当![]() 且
且![]() 为偶数时,
为偶数时, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
⑶ 设数列![]() 的前
的前![]() 项的和为
项的和为![]() ,试求数列
,试求数列![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017安徽蚌埠一模)已知椭圆C:![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,F1,F2是椭圆的两个焦点,P是椭圆上任意一点,且△PF1F2的周长是8+2
,F1,F2是椭圆的两个焦点,P是椭圆上任意一点,且△PF1F2的周长是8+2![]() .
.

(1)求椭圆C的方程;
(2)设圆T:(x-2)2+y2=![]() ,过椭圆的上顶点M作圆T的两条切线交椭圆于E,F两点,求直线EF的斜率.
,过椭圆的上顶点M作圆T的两条切线交椭圆于E,F两点,求直线EF的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥PABC中,不能证明AP⊥BC的条件是( )
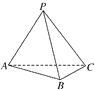
A. AP⊥PB,AP⊥PC
B. AP⊥PB,BC⊥PB
C. 平面BPC⊥平面APC,BC⊥PC
D. AP⊥平面PBC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com