
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的坐标方程为
的坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切.
相切.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在曲线![]() 上取两点
上取两点![]() 、
、![]() 于原点
于原点![]() 构成
构成![]() ,且满足
,且满足![]() ,求面积
,求面积![]() 的最大值.
的最大值.
科目:高中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是
分别是![]() 边上的三等分点,将
边上的三等分点,将![]() 分别沿
分别沿![]() 、
、![]() 折起到
折起到![]() 、
、![]() 的位置,且使平面
的位置,且使平面![]() 底面
底面![]() ,平面
,平面![]() 底面
底面![]() ,连结
,连结![]() .
.
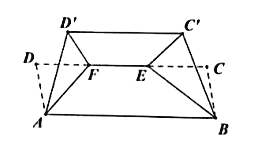
(1)证明:![]() 平面
平面![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]() ,在某一周期内的图象时,列表并填入了部分数据,如下表:
,在某一周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
x |
|
| |||
| 0 | 2 | 0 | 0 |
(1)请将上表数据补充完整,并求函数![]() 的解析式;
的解析式;
(2)求函数![]() 的单调递增区间;
的单调递增区间;
(3)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的偶函数f(x),其导函数![]() ,当x≥0时,恒有
,当x≥0时,恒有![]()
![]() +f(﹣x)<0,若g(x)=x2f(x),则不等式g(x)<g(1﹣2x)的解集为( )
+f(﹣x)<0,若g(x)=x2f(x),则不等式g(x)<g(1﹣2x)的解集为( )
A.(![]() ,1)B.(﹣∞,
,1)B.(﹣∞,![]() )∪(1,+∞)
)∪(1,+∞)
C.(![]() ,+∞)D.(﹣∞,
,+∞)D.(﹣∞,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() :
: ![]() 的离心率
的离心率![]() ,
, ![]() 、
、![]() 为其左右焦点,点
为其左右焦点,点![]() 在
在![]() 上,且
上,且![]() ,
, ![]() ,
, ![]() 是坐标原点.
是坐标原点.
(1)求双曲线![]() 的方程;
的方程;
(2)过![]() 的直线
的直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校大一新生中的6名同学打算参加学校组织的“演讲团”、“吉他协会”等五个社团,若每名同学必须参加且只能参加1个社团且每个社团至多两人参加,则这6个人中没有人参加“演讲团”的不同参加方法数为( )
A. 3600 B. 1080 C. 1440 D. 2520
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,雾霾日趋严重,雾霾的工作、生活受到了严重的影响,如何改善空气质量已成为当今的热点问题,某空气净化器制造厂,决定投入生产某型号的空气净化器,根据以往的生产销售经验得到下面有关生产销售的统计规律,每生产该型号空气净化器![]() (百台),其总成本为
(百台),其总成本为![]() (万元),其中固定成本为12万元,并且每生产1百台的生产成本为10万元(总成本=固定成本+生产成本),销售收入
(万元),其中固定成本为12万元,并且每生产1百台的生产成本为10万元(总成本=固定成本+生产成本),销售收入![]() (万元)满足
(万元)满足![]() ,假定该产品销售平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品销售平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)求利润函数![]() 的解析式(利润=销售收入-总成本);
的解析式(利润=销售收入-总成本);
(2)工厂生产多少百台产品时,可使利润最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代十进制的算筹计数法,在数学史上是一个伟大的创造,算筹实际上是一根根同长短的小木棍.如图,是利用算筹表示数![]() 的一种方法.例如:3可表示为“
的一种方法.例如:3可表示为“![]() ”,26可表示为“
”,26可表示为“![]() ”.现有6根算筹,据此表示方法,若算筹不能剩余,则可以用
”.现有6根算筹,据此表示方法,若算筹不能剩余,则可以用![]() 这9数字表示两位数的个数为
这9数字表示两位数的个数为![]()
![]()
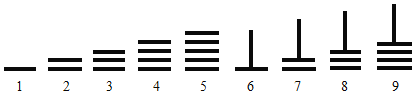
A.13B.14C.15D.16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com