
【题目】已知函数![]() ,
, ![]() ,其中
,其中![]()
(1)设函数![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(2)若存在![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】某地区以“绿色出行”为宗旨开展“共享单车”业务.该地区某高级中学一兴趣小组由9名高二级学生和6名高一级学生组成,现采用分层抽样的方法抽取5人,组成一个体验小组去市场体验“共享单车”的使用.问:
(Ⅰ)应从该兴趣小组中抽取高一级和高二级的学生各多少人;
(Ⅱ)已知该地区有![]() ,
, ![]() 两种型号的“共享单车”,在市场体验中,该体验小组的高二级学生都租
两种型号的“共享单车”,在市场体验中,该体验小组的高二级学生都租![]() 型车,高一级学生都租
型车,高一级学生都租![]() 型车.如果从组内随机抽取2人,求抽取的2人中至少有1人在市场体验过程中租
型车.如果从组内随机抽取2人,求抽取的2人中至少有1人在市场体验过程中租![]() 型车的概率.
型车的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市居民自来水收费标准如下:每户每月用水不超过4吨时,每吨为2.10元,当用水超过4吨时,超过部分每吨3.00元,某月甲、乙两户共交水费y元.已知甲、乙两用户该月用水量分别为5x,3x吨.
(1)求y关于x的函数;
(2)如甲、乙两户该月共交水费40.8元,分别求出甲、乙两户该月的用水量和水费.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)
某公司经销某产品,第![]() 天
天![]() 的销售价格为
的销售价格为![]() (
(![]() 为常数)(元∕件),第
为常数)(元∕件),第![]() 天的销售量为
天的销售量为![]() (件),且公司在第
(件),且公司在第![]() 天该产品的销售收入为
天该产品的销售收入为![]() 元.
元.
(1)求该公司在第![]() 天该产品的销售收入是多少?
天该产品的销售收入是多少?
(2)这![]() 天中该公司在哪一天该产品的销售收入最大?最大收入为多少?
天中该公司在哪一天该产品的销售收入最大?最大收入为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,用K、A1、A2三类不同的元件连接成一个系统.当K正常工作且A1、A2至少有一个正常工作时,系统正常工作,已知K、A1、A2正常工作的概率依次是0.9、0.8、0.8,则系统正常工作的概率为( )
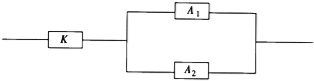
A. 0.960 B. 0.864 C. 0.720 D. 0.576
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .直线
.直线![]() 过点
过点![]() .
.
(1)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值;
的值;
(2)求曲线![]() 的内接矩形的周长的最大值.
的内接矩形的周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
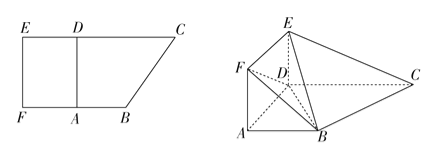
【题目】【2017银川一中模拟】如图,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AB=AD=![]() CD=1.现以AD为一边向梯形外作矩形ADEF,然后沿边AD将矩形ADEF翻折,使平面ADEF与平面ABCD垂直.
CD=1.现以AD为一边向梯形外作矩形ADEF,然后沿边AD将矩形ADEF翻折,使平面ADEF与平面ABCD垂直.
(1)求证:BC⊥平面BDE;
(2)若点D到平面BEC的距离为![]() ,求三棱锥F-BDE的体积.
,求三棱锥F-BDE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了实现60万元的生源利润目标,准备制定一个激励招生人员的奖励方案:在生源利润达到5万元时,按生源利润进行奖励,且资金y(单位:万元)随生源利润x(单位:万元)的增加而增加,但资金总数不超过3万元,同时奖金不超过利润的20%.现有三个奖励模型:y=0.2x,y=log5x,y=1.02x,其中哪个模型符合该校的要求?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com