
【题目】已知函数![]() ,
,![]() 为偶函数,且当
为偶函数,且当![]() 时,
时,![]() .记
.记![]() .给出下列关于函数
.给出下列关于函数![]() 的说法:①当
的说法:①当![]() 时,
时,![]() ;②函数
;②函数![]() 为奇函数;③函数
为奇函数;③函数![]() 在
在![]() 上为增函数;④函数
上为增函数;④函数![]() 的最小值为
的最小值为![]() ,无最大值.其中正确的是______.
,无最大值.其中正确的是______.
【答案】①③
【解析】
g(x)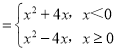 ,F(x)=max{f(x),g(x)}(x∈R)
,F(x)=max{f(x),g(x)}(x∈R)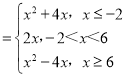 .画出图象,数形结合即可得出.
.画出图象,数形结合即可得出.
由![]() 为偶函数,且当
为偶函数,且当![]() 时,
时,![]() ,
,
∴令![]() ,则
,则![]() ,则
,则![]() ,
,
即当![]() 时,
时,![]() ,
,
∴g(x)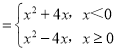 ,
,
F(x)=max{f(x),g(x)}(x∈R)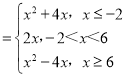 .
.
画出图象,
由图象可得:①当x≥6时,∵x2﹣4x≥2x,∴F(x)=x2﹣4x,因此正确.
②由图象可得:函数F(x)不为奇函数,因此不正确.
③﹣2≤x≤6时,2x>x2﹣4x,可得函数F(x)=2x,因此函数F(x)在[﹣2,6]上为增函数,所以函数F(x)在[﹣2,2]上为增函数是正确的.
④x≤﹣2时,g(x)=x2+4x≥2x,可得F(x)=x2+4x≥﹣4,综合可得函数F(x)的最小值为﹣4,无最大值,④不正确.
其中正确的是 ①③.
故答案为①③.


科目:高中数学 来源: 题型:
【题目】已知向量![]() = (1,2sinθ),
= (1,2sinθ),![]() = (sin(θ+
= (sin(θ+![]() ),1),θ
),1),θ![]() R。
R。
(1) 若![]() ⊥
⊥![]() ,求 tanθ的值;
,求 tanθ的值;
(2) 若![]() ∥
∥![]() ,且 θ
,且 θ![]() (0,
(0,![]() ),求 θ的值
),求 θ的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某地区乡居民人民币储蓄存款(年底余额)如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
时间代号 | 1 | 2 | 3 | 4 | 5 | 6 |
储蓄存款 | 3.5 | 5 | 6 | 7 | 8 | 9.5 |
(1)求关于![]() 的回归方程
的回归方程![]() ,并预测该地区2019年的人民币储蓄存款(用最简分数作答).
,并预测该地区2019年的人民币储蓄存款(用最简分数作答).
(2)在含有一个解释变量的线性模型中,![]() 恰好等于相关系数
恰好等于相关系数![]() 的平方,当
的平方,当![]() 时,认为线性回归模型是有效的,请计算
时,认为线性回归模型是有效的,请计算![]() 并且评价模型的拟合效果(计算结果精确到
并且评价模型的拟合效果(计算结果精确到![]() ).
).
附:
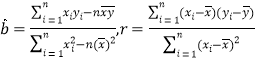 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
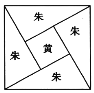
【题目】《周髀算经》中给出了勾股定理的绝妙证明.下图是赵爽弦图及注文,弦图是一个以勾股形之弦为边的正方形,其面积称为弦实,图中包含四个全等的勾股形及一个小正方形,分别涂成朱色及黄色,其面积称为朱实、黄实.由2![]() 勾
勾![]() 股
股![]() (股
(股![]() 勾)2
勾)2![]() 4
4![]() 朱实
朱实![]() 黄实
黄实![]() 弦实,化简得勾2
弦实,化简得勾2![]() 股2
股2![]() 弦2.若图中勾股形的勾股比为
弦2.若图中勾股形的勾股比为![]() ,若向弦图内随机抛掷2000颗图钉(大小忽略不计),则落在黄色图形内的图钉颗数大约为( )(参考数据:
,若向弦图内随机抛掷2000颗图钉(大小忽略不计),则落在黄色图形内的图钉颗数大约为( )(参考数据:![]() )
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某动漫影视制作公司长期坚持文化自信,不断挖掘中华优秀传统文化中的动漫题材,创作出一批又一批的优秀动漫影视作品,获得市场和广大观众的一致好评.同时也为公司赢得丰厚的利润,该公司2013年至2019年的年利润![]() 关于年份代号
关于年份代号![]() 的统计数据如下表(已知该公司的年利润与年份代号线性相关)
的统计数据如下表(已知该公司的年利润与年份代号线性相关)
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
年利润 | 29 | 33 | 36 | 44 | 48 | 52 | 59 |
(1)求![]() 关于
关于![]() 的线性回归方程,并预测该公司2020年的年利润;
的线性回归方程,并预测该公司2020年的年利润;
(2)当统计表中某年年利润的实际值大于由(1)中线性回归方程计算出该年利润的估计值时,称该年为A级利润年,否则称为B级利润年.现从2015年至2019年这5年中随机抽取2年,求恰有1年为A级利润年的概率.
参考公式: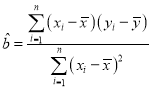 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于古典概型的说法中正确的是( )
①试验中所有可能出现的基本事件只有有限个;
②每个事件出现的可能性相等;
③每个基本事件出现的可能性相等;
④基本事件的总数为n,随机事件A若包含k个基本事件,则![]() .
.
A. ②④ B. ③④ C. ①④ D. ①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生产厂家生产一种产品的固定成本为4万元,并且每生产1百台产品需增加投入0.8万元.已知销售收入![]() (万元)满足
(万元)满足![]() (其中
(其中![]() 是该产品的月产量,单位:百台),假定生产的产品都能卖掉,请完成下列问题:
是该产品的月产量,单位:百台),假定生产的产品都能卖掉,请完成下列问题:
(1)将利润表示为月产量![]() 的函数
的函数![]() ;
;
(2)当月产量为何值时,公司所获利润最大?最大利润为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() 为椭圆
为椭圆![]() 的左焦点,直线
的左焦点,直线![]() 被椭圆
被椭圆![]() 截得弦长为
截得弦长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)圆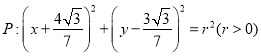 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点, ![]() 为线段
为线段![]() 上任意一点,直线
上任意一点,直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点
两点![]() 为圆
为圆![]() 的直径,且直线
的直径,且直线![]() 的斜率大于
的斜率大于![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com