练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】中国的嫦娥四号探测器，简称“四号星”，是世界首个在月球背面软着陆和巡视探测的航天器.2019年9月25日，中国科研人员利用嫦娥四号数据精确定位了嫦娥四号的着陆位置，并再现了嫦娥四号的落月过程，该成果由国际科学期刊《自然·通讯》在线发表.如图所示，

    现假设“四号星”沿地月转移轨道飞向月球后，在月球附近一点变轨进入以月球球心为一个焦点的椭圆轨道Ⅰ绕月飞行，之后卫星在点第二次变轨进入仍以为一个焦点的椭圆轨道Ⅱ绕月飞行.若用和分别表示椭圆轨道Ⅰ和Ⅱ的焦距，用和分别表示椭圆轨道Ⅰ和Ⅱ的长轴长，给出下列式子：①；②；③；④.其中正确的式子的序号是（ ）

    A.①③B.①④C.②③D.②④

    【答案】D

    【解析】

    根据图形关系分析，，辨析为平方处理，结合即可得到离心率的关系.

    由图可知：所以，所以①不正确；

    在椭圆轨道Ⅰ中可得：，椭圆轨道Ⅱ中可得：，

    所以，所以②正确；

    ，同时平方得：，

    所以，

    即，由图可得：，

    所以，，所以③错误，④正确.

    故选：D

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）若，函数在上有三个零点，求实数的取值范围；

    （2）若常数，且对任何，不等式恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝|x＋m|＋|2x－1|.

    (1)当m＝－1时，求不等式f(x)≤2的解集；

    (2)若f(x)≤|2x＋1|的解集包含，求m的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数().

    （1）讨论的单调性；

    （2）若对，恒成立，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，直线的倾斜角为，且经过点．以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，直线，从原点O作射线交于点M，点N为射线OM上的点，满足，记点N的轨迹为曲线C．

    （Ⅰ）求出直线的参数方程和曲线C的直角坐标方程；

    （Ⅱ）设直线与曲线C交于P，Q两点，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】把参加某次铅球投掷的同学的成绩(单位：米)进行整理，分成以下6个小组：[5.25，6.15)，[6.15，7.05)，[7.05，7.95)，[7.95，8.85)，[8.85，9.75)，[9.75，10.65]，并绘制出频率分布直方图，如图所示是这个频率分布直方图的一部分．已知从左到右前5个小组的频率分别为0.04，0.10，0.14，0.28，0.30，第6小组的频数是7．规定：投掷成绩不小于7.95米的为合格．

    (1)求这次铅球投掷成绩合格的人数；

    (2)你认为这次铅球投掷的同学的成绩的中位数在第几组？请说明理由；

    (3)若参加这次铅球投掷的学生中，有5人的成绩为优秀，现在要从成绩优秀的学生中，随机选出2人参加相关部门组织的经验交流会，已知a、b 两位同学的成绩均为优秀，求a、b 两位同学中至少有1人被选到的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某医院体检中心为回馈大众，推出优惠活动：对首次参加体检的人员，按200元次收费，并注册成为会员，对会员的后续体检给予相应优惠，标准如下：

    体检次序

    第一次

    第二次

    第三次

    第四次

    第五次及以上

    收费比例

    1

    0.95

    0.90

    0.85

    0.8

    该体检中心从所有会员中随机选取了100位对他们在本中心参加体检的次数进行统计，得到数据如下表：

    体检次数

    一次

    两次

    三次

    四次

    五次及以上

    频数

    60

    20

    10

    5

    5

    假设该体检中心为顾客体检一次的成本费用为150元，根据所给数据，解答下列问题：

    （1）该体检中心要从这100人里至少体检3次的会员中，按体检次数用分层抽样的方法抽出8人，再从这8人中抽出2人发放纪念品，求抽出的2人中恰有1人体检3次的概率；

    （2）若以这100位会员体检次数的频率分布估计该体检中心所有会员体检次数的概率分布，已知该中心本周共接待了1000名顾客参加体检，试估计该体检中心本周所获利润.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

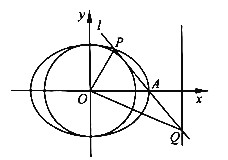
    【题目】在平面直角坐标系中，已知椭圆的右顶点为，过点作直线与圆相切，与椭圆交于另一点，与右准线交于点.设直线的斜率为.

    （1）用表示椭圆的离心率；

    （2）若，求椭圆的离心率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

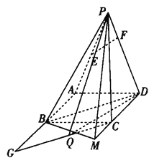
    【题目】如图，在四棱锥中，四边形是边长为2的正方形，，为的中点，点在上，平面，在的延长线上，且.

    (1)证明:平面.

    (2)过点作的平行线，与直线相交于点，点为的中点，求到平面的距离.

    查看答案和解析>>

    同步练习册答案