
【题目】已知函数f(x)=|2x﹣a|+|x﹣a+1|.
(1)当a=4时,求解不等式f(x)≥8;
(2)已知关于x的不等式f(x)![]() 在R上恒成立,求参数a的取值范围.
在R上恒成立,求参数a的取值范围.
【答案】(1)[5,+∞)∪(∞,![]() ];(2)[﹣2,1].
];(2)[﹣2,1].
【解析】
(1)根据a=4时,有f(x)=|2x﹣4|+|x﹣3|,然后利用绝对值的几何意义,去绝对值求解.
(2)根据绝对值的零点有a﹣1和![]() ,分a﹣1
,分a﹣1![]() ,a﹣1
,a﹣1![]() 和a﹣1
和a﹣1![]() 时三种情况分类讨论求解.
时三种情况分类讨论求解.
(1)当a=4时,f(x)=|2x﹣4|+|x﹣3|,
(i)当x≥3时,原不等式可化为3x﹣7≥8,解可得x≥5,
此时不等式的解集[5,+∞);
(ii)当2<x<3时,原不等式可化为2x﹣4+3﹣x≥8,解可得x≥9
此时不等式的解集;
(iii)当x≤2时,原不等式可化为﹣3x+7≥8,解可得x![]() ,
,
此时不等式的解集(∞,![]() ],
],
综上可得,不等式的解集[5,+∞)∪(∞,![]() ],
],
(2)(i)当a﹣1![]() 即a=2时,f(x)=3|x﹣1|
即a=2时,f(x)=3|x﹣1|![]() 2显然不恒成立,
2显然不恒成立,
(ii)当a﹣1![]() 即a>2时,
即a>2时, ,
,
结合函数的单调性可知,当x![]() 时,函数取得最小值f(
时,函数取得最小值f(![]() )
)![]() ,
,
若f(x)![]() 在R上恒成立,则
在R上恒成立,则![]() ,此时a不存在,
,此时a不存在,
(iii)当a﹣1![]() 即a<2时,f(x)
即a<2时,f(x)
若f(x)![]() 在R上恒成立,则1
在R上恒成立,则1![]() ,
,
解得﹣2≤a≤1,
此时a的范围[﹣2,1],
综上可得,a的范围围[﹣2,1].


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为:
的极坐标方程为:![]() .
.
(Ⅰ)求直线![]() 与曲线
与曲线![]() 公共点的极坐标;
公共点的极坐标;
(Ⅱ)设过点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知顶点为原点的抛物线C的焦点与椭圆![]() 的上焦点重合,且过点
的上焦点重合,且过点![]() .
.
(1)求椭圆的标准方程;
(2)若抛物线上不同两点A,B作抛物线的切线,两切线的斜率![]() ,若记AB的中点的横坐标为m,AB的弦长
,若记AB的中点的横坐标为m,AB的弦长![]() ,并求
,并求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大约在20世纪30年代,世界上许多国家都流传着这样一个题目:任取一个正整数![]() ,如果它是偶数,则除以2;如果它是奇数,则将它乘以3加1,这样反复运算,最后结果必然是1.这个题目在东方被称为“角谷猜想”,世界一流的大数学家都被其卷入其中,用尽了各种方法,甚至动用了最先进的电子计算机,验算到对700亿以内的自然数上述结论均为正确的,但却给不出一般性的证明.例如取
,如果它是偶数,则除以2;如果它是奇数,则将它乘以3加1,这样反复运算,最后结果必然是1.这个题目在东方被称为“角谷猜想”,世界一流的大数学家都被其卷入其中,用尽了各种方法,甚至动用了最先进的电子计算机,验算到对700亿以内的自然数上述结论均为正确的,但却给不出一般性的证明.例如取![]() ,则要想算出结果1,共需要经过的运算步数是( )
,则要想算出结果1,共需要经过的运算步数是( )
A.9B.10C.11D.12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 与直线l:y=kx﹣1无交点,设点P为直线l上的动点,过P作抛物线C的两条切线,A,B为切点.
与直线l:y=kx﹣1无交点,设点P为直线l上的动点,过P作抛物线C的两条切线,A,B为切点.
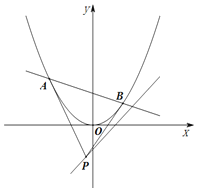
(1)证明:直线AB恒过定点Q;
(2)试求△PAB面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭记录了未使用节水龙头50天的日用水量数据(单位:m3)和使用了节水龙头50天的日用水量数据,得到频数分布表如下:
未使用节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
|
频数 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
使用了节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
频数 | 1 | 5 | 13 | 10 | 16 | 5 |
(1)在答题卡上作出使用了节水龙头50天的日用水量数据的频率分布直方图:
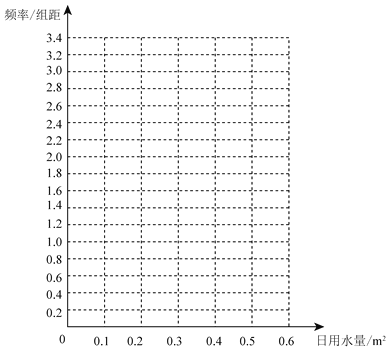
(2)估计该家庭使用节水龙头后,日用水量小于0.35 m3的概率;
(3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于圆周率![]() ,数学发展史上出现过许多有创意的求法,如著名的普丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计
,数学发展史上出现过许多有创意的求法,如著名的普丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计![]() 的值:先请120名同学每人随机写下一个x,y都小于1的正实数对
的值:先请120名同学每人随机写下一个x,y都小于1的正实数对![]() ,再统计其中x,y能与1构成钝角三角形三边的数对
,再统计其中x,y能与1构成钝角三角形三边的数对![]() 的个数m,最后根据统计个数m估计
的个数m,最后根据统计个数m估计![]() 的值.如果统计结果是
的值.如果统计结果是![]() ,那么可以估计
,那么可以估计![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com