
【题目】已知a≠0,集合A={x|x2﹣x﹣6<0},B={x|x2+2x﹣8≥0},C={x|x2﹣4ax+3a2<0},且C(A∩RB).求实数a的取值范围.
【答案】解:依题意得:A={x|﹣2<x<3},B={x|x≤﹣4或x≥2},(CRB)={x|﹣4<x<2}
∴A∩(CRB)=(﹣2,2)
①若a>0,则C={x|a<x<3a},
由C(A∩CRB)得 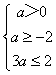 ,解得0<a≤
,解得0<a≤ ![]()
②若a<0,则C={x|3a<x<a},
由C(A∩CRB)得  ,解得﹣
,解得﹣ ![]() ≤a<0
≤a<0
综上,实数a的取值范围为0<a≤ ![]() 或﹣
或﹣ ![]() ≤a<0
≤a<0
【解析】先通过解一元二次不等式化简集合A和B,再求集合B的补集,最后求出A∩(CRB),由于一元二次方程x2﹣4ax+3a2=0的两个根是:a,3a.欲表示出集合C,须对a进行分类讨论:①若a>0,②若a<0,再结合C(A∩CRB),列出不等关系求得a的取值范围,最后综合得出实数a的取值范围即可.
【考点精析】本题主要考查了交、并、补集的混合运算的相关知识点,需要掌握求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】在正三棱柱ABC﹣A1B1C1中,若AB1⊥BC1 , 则下列关于直线A1C和AB1 , BC1的关系的判断正确的为( )
A.A1C和AB1 , BC1都垂直
B.A1C和AB1垂直,和BC1不垂直
C.A1C和AB1 , BC1都不垂直
D.A1C和AB1不垂直,和BC1垂直
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域是(0,+∞),对于任意正实数m,n恒有f(mn)=f(m)+f(n),且当x>1时,f(x)>0,f(2)=1.
(1)求 ![]() 的值;
的值;
(2)求证:f(x)在(0,+∞)上是增函数;
(3)求方程4sinx=f(x)的根的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣x2+2ex﹣x﹣ ![]() +m (x>0),若f(x)=0有两个相异实根,则实数m的取值范围是( )
+m (x>0),若f(x)=0有两个相异实根,则实数m的取值范围是( )
A.(﹣e2+2e,0)
B.(﹣e2+2e,+∞)
C.(0,e2﹣2e)
D.(﹣∞,﹣e2+2e)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面是边长为a的正方形,PB⊥平面ABCD,M、N分别是AB、PC的中点. 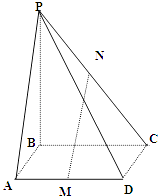
(1)求证:MN∥平面PAB;
(2)若平面PDA与平面ABCD成60°的二面角,求该四棱锥的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,侧面PAB⊥底面ABCD.若PA=AD=AB=kBC(0<k<1),则( ) 
A.当k= ![]() 时,平面BPC⊥平面PCD
时,平面BPC⊥平面PCD
B.当k= ![]() 时,平面APD⊥平面PCD
时,平面APD⊥平面PCD
C.对?k∈(0,1),直线PA与底面ABCD都不垂直
D.?k∈(0,1),使直线PD与直线AC垂直.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直线 l1和l2 是异面直线,l1在平面 α内,l2在平面β内,l是平面α与平面β的交线,则下列命题正确的是( )
A.l与l1 , l2都不相交
B.l与l1 , l2都相交
C.l至多与l1 , l2中的一条相交
D.l至少与l1 , l2中的一条相交
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥S﹣ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是( ) 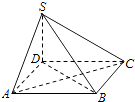
A.AC⊥SB
B.AB∥平面SCD
C.SA与平面SBD所成的角等于SC与平面SBD所成的角
D.AB与SC所成的角等于DC与SA所成的角
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com