
【题目】已知函数![]() .
.
(1)证明:函数![]() 在
在![]() 上单调递增;
上单调递增;
(2)若![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)详见解析;(2)![]() .
.
【解析】
试题解析:(1)求导![]() ,判断其符号,可知函数
,判断其符号,可知函数![]() 在
在![]() 上单调递增;
上单调递增;
(2)由(1)得![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,所以
,所以![]() ,分类讨论
,分类讨论
(ⅰ)当![]() 时,
时,![]() 成立.
成立.
(ⅱ)当![]() 时,
时,
构造函数![]() ,利用导数讨论其单调性,可知
,利用导数讨论其单调性,可知![]() 时,
时,![]() .(*)
.(*)
由(*)式可得![]() ,
,
令![]() ,求导
,求导![]()
由(*)式可得![]() ,
,
令![]() ,得
,得![]() 在
在![]() 上单调递增,研究函数
上单调递增,研究函数![]() 的性质可知
的性质可知
存在 ![]() 使得
使得![]() ,即
,即![]() 时,
时,![]() ,
,
即![]() 时,
时,![]() ,
,![]() 单调递减,又
单调递减,又![]() ,所以
,所以![]() ,
,
即![]() 时,
时,![]() ,与
,与![]() 矛盾.
矛盾.
综上,满足条件的![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(1)![]() ,
,
因为![]() ,所以
,所以![]() ,于是
,于是
![]() (等号当且仅当
(等号当且仅当![]() 时成立).
时成立).
故函数![]() 在
在![]() 上单调递增.
上单调递增.
(2)由(Ⅰ)得![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,所以
,所以![]() ,
,
(ⅰ)当![]() 时,
时,![]() 成立.
成立.
(ⅱ)当![]() 时,
时,
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递减,又
单调递减,又![]() ,所以
,所以![]() ,
,
故![]() 时,
时,![]() .(*)
.(*)
由(*)式可得![]() ,
,
令![]() ,则
,则![]()
由(*)式可得![]() ,
,
令![]() ,得
,得![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,
,![]() ,所以存在
,所以存在 ![]() 使得
使得![]() ,即
,即![]() 时,
时,![]() ,
,
所以![]() 时,
时,![]() ,
,![]() 单调递减,又
单调递减,又![]() ,所以
,所以![]() ,
,
即![]() 时,
时,![]() ,与
,与![]() 矛盾.
矛盾.
综上,满足条件的![]() 的取值范围是
的取值范围是![]() .
.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
【题目】给出下面四个命题:
①“直线![]() 平面
平面![]() 内所有直线”的充要条件是“
内所有直线”的充要条件是“![]() 平面
平面![]() ”;
”;
②“直线![]() 直线
直线![]() ”的充要条件是“
”的充要条件是“![]() 平行于
平行于![]() 所在的平面”;
所在的平面”;
③“直线![]() ,
,![]() 为异面直线”的充分不必要条件是“直线
为异面直线”的充分不必要条件是“直线![]() ,
,![]() 不相交”;
不相交”;
④“平面![]() 平面
平面![]() ”的必要不充分条件是“
”的必要不充分条件是“![]() 内存在不共线三点到
内存在不共线三点到![]() 的距离相等”.
的距离相等”.
其中正确命题的序号是____________________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() 为椭圆
为椭圆![]() 的左焦点,直线
的左焦点,直线![]() 被椭圆
被椭圆![]() 截得弦长为
截得弦长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)圆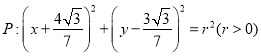 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点, ![]() 为线段
为线段![]() 上任意一点,直线
上任意一点,直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点
两点![]() 为圆
为圆![]() 的直径,且直线
的直径,且直线![]() 的斜率大于
的斜率大于![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若椭圆![]() :
:![]() (
(![]() )与椭圆
)与椭圆![]() :
:![]() (
(![]() )的焦距相等,给出如下四个结论:
)的焦距相等,给出如下四个结论:
①![]() 和
和![]() 一定有交点;
一定有交点;
②若![]() ,则
,则![]() ;
;
③若![]() ,则
,则![]() ;
;
④设![]() 与
与![]() 在第一象限内相交于点
在第一象限内相交于点![]() ,若
,若![]() ,则
,则![]() .
.
其中,所有正确结论的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在矩形![]() 中,
中,![]() ,沿直线BD将△ABD折成
,沿直线BD将△ABD折成![]() ,使得点
,使得点![]() 在平面
在平面![]() 上的射影在
上的射影在![]() 内(不含边界),设二面角
内(不含边界),设二面角![]() 的大小为
的大小为![]() ,直线
,直线![]() ,
,![]() 与平面
与平面![]() 中所成的角分别为
中所成的角分别为![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】港珠澳大桥是中国建设史上里程最长,投资最多,难度最大的跨海桥梁项目,大桥建设需要许多桥梁构件。从某企业生产的桥梁构件中抽取![]() 件,测量这些桥梁构件的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间
件,测量这些桥梁构件的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间![]() ,
,![]() ,
,![]() 内的频率之比为
内的频率之比为![]() .
.
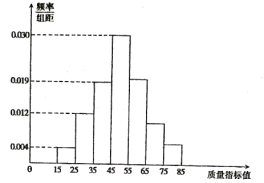
(1)求这些桥梁构件质量指标值落在区间![]() 内的频率;
内的频率;
(2)用分层抽样的方法在区间![]() 内抽取一个容量为
内抽取一个容量为![]() 的样本,将该样本看成一个总体,从中任意抽取
的样本,将该样本看成一个总体,从中任意抽取![]() 件桥梁构件,求这
件桥梁构件,求这![]() 件桥梁构件都在区间
件桥梁构件都在区间![]() 内的概率
内的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com