【题目】如图，在三棱锥
中，已知
平面
， 
， 
， 
， 
．
（I）求证： 
平面
；
（II）求直线
与平面
所成角的正弦值．
【答案】(Ⅰ)见解析(Ⅱ) 
【解析】试题分析：(Ⅰ)由线面垂直的性质可得
，结合已知
，根据线面垂直的判定定理可得结论；(Ⅱ) 由(I)可得
即为直线
与平面
所成的角，在直角三角形
中，可得
.
试题解析：(Ⅰ) 证明：因为
平面
， 
平面
，所以
，又因为
， 
，所以
平面
．
(Ⅱ) 解：由(I)可得
即为直线
与平面
所成的角，由已知得
， 
，所以在直角三角形
中， 
，即直线
与平面
所成的角的正弦值为
．
【方法点晴】本题主要考查线面垂直的判定定理及线面角的求法，属于中档题. 解答空间几何体中垂直关系时，一般要根据已知条件把空间中的线线、线面、面面之间垂直关系进行转化，转化时要正确运用有关的定理，找出足够的条件进行推理；证明直线和平面垂直的常用方法有：（1）利用判定定理；（2）利用判定定理的推论
；（3）利用面面平行的性质
；（4）利用面面垂直的性质，当两个平面垂直时，在一个平面内垂直于交线的直线垂直于另一个平面.
快乐小博士巩固与提高系列答案科目：高中数学 来源： 题型：
【题目】某地区交管部门为了对该地区驾驶员的某项考试成绩进行分析，随机抽取了15分到45分之间的1000名学员的成绩，并根据这1000名驾驶员的成绩画出样本的频率分布直方图（如图），则成绩在[30，35）内的驾驶员人数共有（ ） 
A.60
B.180
C.300
D.360
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，
为正方体，给出以下五个结论：
① 
平面
；
② 
⊥平面；
③ 与底面
所成角的正切值是
；
④ 二面角
的正切值是；
⑤ 过点
且与异面直线
和 
均成70°角的直线有4条．
其中，所有正确结论的序号为________．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】以坐标原点为极点，x轴的正半轴为极轴建立极坐标系．已知曲线C的参数方程为： 
（φ为参数），直线l的极坐标方程为ρ（cosθ+sinθ）=4．
（1）求曲线C的普通方程和直线l的直角坐标方程；
（2）若点P在曲线C上，点Q在直线l上，求线段PQ的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知直线
： 
与抛物线
交于
， 
两点，记抛物线在
， 
两点处的切线
， 
的交点为
．
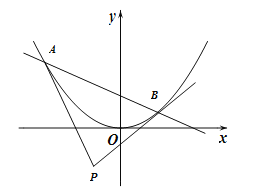
（I）求证: 
；
（II）求点
的坐标(用
， 
表示)；
（Ⅲ）若
，求△
的面积的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知平面内圆心为
的圆的方程为
，点
是圆上的动点，点
是平面内任意一点，若线段
的垂直平分线交直线
于点
，则点
的轨迹可能是_________．（请将下列符合条件的序号都填入横线上）
①椭圆；②双曲线；③抛物线；④圆；⑤直线；⑥一个点.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】函数f（x）= 
若a，b，c，d各不相同，且f（a）=f（b）=f（c）=f（d），则abcd的取值范围是（ ）
A.（24，25）
B.[16，25）
C.（1，25）
D.（0，25]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
