
分析 对任意的正整数n,满足an+2-an≤3n,可得an+4-an+2≤3n+2,an+4-an≤10×3n,又an+4-an≥10×3n,则an+4-an=10×3n,利用“累加求和”方法即可得出.
解答 解:∵对任意的正整数n,满足an+2-an≤3n,∴an+4-an+2≤3n+2.
∴an+4-an≤10×3n,
又an+4-an≥10×3n,则an+4-an=10×3n,
∴a8-a4=10×34,a12-a8=10×38,…,a2016-a2012=10×32012.
∴a2016-a4=10×(34+38+…+32012)=10×$\frac{81(8{1}^{503}-1)}{81-1}$=$\frac{81(8{1}^{503}-1)}{8}$.
∴a2016=a4+$\frac{81(8{1}^{503}-1)}{8}$=$\frac{8{1}^{504}-80}{8}$.
故答案为:$\frac{8{1}^{504}-80}{8}$.
点评 本题考查了数列递推关系、“累加求和”方法、不等式的性质,考查了推理能力与计算能力,属于中档题.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:选择题
| A. | [-3,0) | B. | [-3,0] | C. | (0,+∞) | D. | [-3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,+∞) | B. | (-∞,2] | C. | (-∞,-1)和(1,2) | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 级数 | 全月应纳税所得额 | 税率(%) |
| 1 | 不超过1500元的部分 | 3 |
| 2 | 超过1500不超过4500元的部分 | 10 |
| 3 | 超过4500不超过9000元的部分 | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
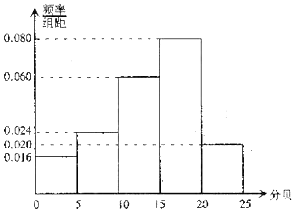 人耳的听力情况可以用电子测听器检测,正常人听力的等级为0-25db(分贝),并规定测试值在区间(0,5]为非常优秀,测试值在区间(5,10]为优秀,某班50名同学都进行了听力测试,所得测试值制成频率分布直方图:
人耳的听力情况可以用电子测听器检测,正常人听力的等级为0-25db(分贝),并规定测试值在区间(0,5]为非常优秀,测试值在区间(5,10]为优秀,某班50名同学都进行了听力测试,所得测试值制成频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
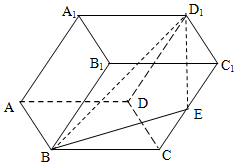 已知斜四棱柱平面ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,
已知斜四棱柱平面ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com