(本小题满分12分)
设函数
f(
x)=
ax+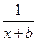
(
a,
b∈Z),曲线
y=
f(
x)在点(2,
f(2))处的切线方程为
y=3。
(Ⅰ)求
f(
x)的解析式:
(Ⅱ)证明:函数
y=
f(
x)的图像是一个中心对称图形,并求其对称中心;
(Ⅲ)证明:曲线
y=f(
x)上任一点的切线与直线
x=1和直线
y=
x所围三角形的面积为定值,并求出此定值。
(Ⅰ)
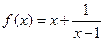
(Ⅱ)证明见解析。
(Ⅲ)证明见解析。
(Ⅰ)
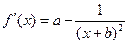
,
于是
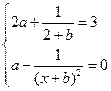
。
解得
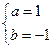
或
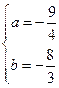
。
因

,故
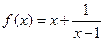
。
(II)证明:已知函数
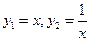
都是奇函数,
所以函数

也是奇函数,其图像是以原点为中心的中心对称图形。
而函数
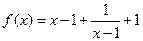
。
可知,函数
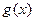
的图像按向量
a=(1,1)平移,即得到函数的图象,故函数
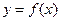
的图像是以点(1,1)为中心的中心对称图形。
(III)证明:在曲线上任一点
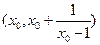
。
由
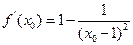
知,过此点的切线方程为
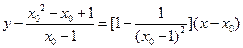
。
令
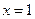
得
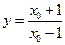
,切线与直线
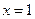
交点为
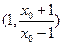
。
令
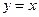
得
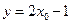
,切线与直线
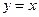
交点为
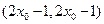
。
直线
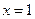
与直线
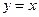
的交点为(1,1)。
从而所围三角形的面积为
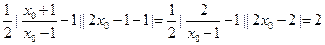
。
所以,所围三角形的面积为定值2。
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:单选题
f(x)=x
3+ax
2+bx+a
2在x=1有极值10,那么a+b的值为 ( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分)
已知函数
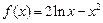
(1)若方程
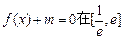
内有两个不等的实根,求实数m的取值范围;(
e为自然对数的底数)
(2)

如果函数
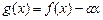
的图象与
x轴交于两点
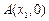
、
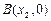
且
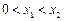
.求证:
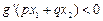
(其中正常数
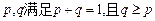
).
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题共13分)
已知函数
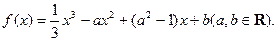
(I)若
x=1为
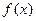
的极值点,求
a的值;
(II)若
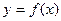
的图象在点(1,
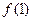
)处的切线方程为
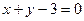
,求
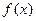
在区间[-2,4]上的最大值;
(III)当
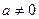
时,若
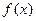
在区间(-1,1)上不单调,求
a的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
求正弦函数
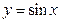
在
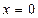
和
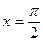
附近的平均变化率,并比较它们的大小.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
曲线
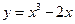
在点
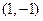
处的切线方程是( ).
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知
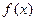
是定义在R上的偶函数,对任意的
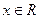
,都有
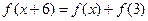
成立,若
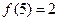
,则
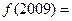
查看答案和解析>>

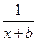 (a,b∈Z),曲线y=f(x)在点(2,f(2))处的切线方程为y=3。
(a,b∈Z),曲线y=f(x)在点(2,f(2))处的切线方程为y=3。 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案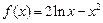
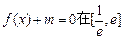 内有两个不等的实根,求实数m的取值范围;(e为自然对数的底数)
内有两个不等的实根,求实数m的取值范围;(e为自然对数的底数) 如果函数
如果函数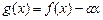 的图象与x轴交于两点
的图象与x轴交于两点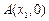 、
、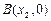 且
且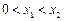 .求证:
.求证: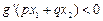 (其中正常数
(其中正常数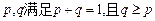 ).
).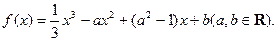
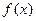 的极值点,求a的值;
的极值点,求a的值;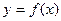 的图象在点(1,
的图象在点(1,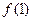 )处的切线方程为
)处的切线方程为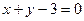 ,求
,求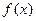 在区间[-2,4]上的最大值;
在区间[-2,4]上的最大值;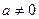 时,若
时,若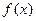 在区间(-1,1)上不单调,求a的取值范围.
在区间(-1,1)上不单调,求a的取值范围.