
【题目】双曲线![]() 的左、右焦点分别是
的左、右焦点分别是![]() ,抛物线
,抛物线![]() 的焦点与点
的焦点与点![]() 重合,点
重合,点![]() 是抛物线与双曲线的一个交点,如图所示.
是抛物线与双曲线的一个交点,如图所示.
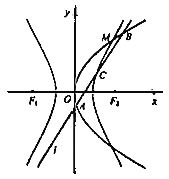
(1)求双曲线及抛物线的标准方程;
(2)设直线![]() 与双曲线的过一、三象限的渐近线平行,且交抛物线于
与双曲线的过一、三象限的渐近线平行,且交抛物线于![]() 两点,交双曲线于点
两点,交双曲线于点![]() ,若点
,若点![]() 是线段
是线段![]() 的中点,求直线
的中点,求直线![]() 的方程.
的方程.
科目:高中数学 来源: 题型:
【题目】在第二届乌镇互联网大会中, 为了提高安保的级别同时又为了方便接待,现将其中的五个参会国的人员安排酒店住宿,这五个参会国要在![]() 、
、![]() 、
、![]() 三家酒店选择一家,且每家酒店至少有一个参会国入住,则这样的安排方法共有
三家酒店选择一家,且每家酒店至少有一个参会国入住,则这样的安排方法共有
A.![]() 种B.
种B.![]() 种
种
C.![]() 种D.
种D.![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲题型:给出如图数阵表格形式,表格内是按某种规律排列成的有限个正整数.
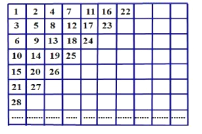
(1)记第一行的自左至右构成数列![]() ,
,![]() 是
是![]() 的前
的前![]() 项和,试求;
项和,试求;
(2)记![]() 为第
为第![]() 列第
列第![]() 行交点的数字,观察数阵请写出
行交点的数字,观察数阵请写出![]() 表达式,若
表达式,若![]() ,试求出
,试求出![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学举行了一次“数学基础知识竞赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为![]() )进行统计.按照
)进行统计.按照![]() 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在![]() 的数据).
的数据).
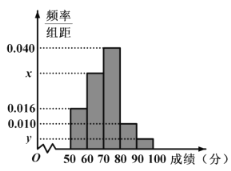

(1)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() ,
,![]() 的值;
的值;
(2)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生参加“市级数学基础知识竞赛”,求所抽取的2名学生中恰有一人得分在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若某产品的直径长与标准值的差的绝对值不超过![]() 时,则视为合格品,否则视为不合格品.在近期一次产品抽样检查中,从某厂生产的此种产品中,随机抽取5000件进行检测,结果发现有50件不合格品.计算这50件不合格品的直径长与标准值的差(单位:
时,则视为合格品,否则视为不合格品.在近期一次产品抽样检查中,从某厂生产的此种产品中,随机抽取5000件进行检测,结果发现有50件不合格品.计算这50件不合格品的直径长与标准值的差(单位:![]() )将所得数据分组,得到如下频率分布表:
)将所得数据分组,得到如下频率分布表:
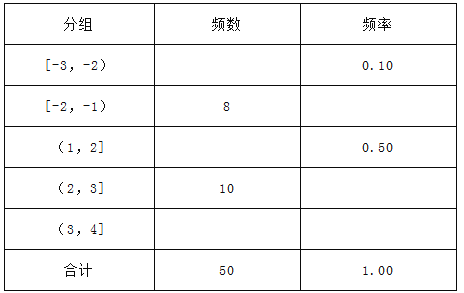
(1)将上面表格中缺少的数据填充完整;
(2)估计该厂生产的此种产品中,不合格的直径长与标准值的差落在区间![]() 内的概率
内的概率
(3)现对该厂这种产品的某个批次进行检查,结果发现有20件不合格品,据此估算这批产品中的合格品的件数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校计划面向高一年级![]() 名学生开设校本选修课程,为确保工作的顺利实施,先按性别进行分层抽样,抽取了
名学生开设校本选修课程,为确保工作的顺利实施,先按性别进行分层抽样,抽取了![]() 名学生对社会科学类,自然科学类这两大类校本选修课程进行选课意向调查,其中男生有
名学生对社会科学类,自然科学类这两大类校本选修课程进行选课意向调查,其中男生有![]() 人.在这
人.在这![]() 名学生中选择社会科学类的男生、女生均为
名学生中选择社会科学类的男生、女生均为![]() 人.
人.
(Ⅰ)分别计算抽取的样本中男生及女生选择社会科学类的频率,并以统计的频率作为概率,估计实际选课中选择社会科学类学生数;
(Ⅱ)根据抽取的![]() 名学生的调查结果,完成下列列联表.并判断能否在犯错误的概率不超过
名学生的调查结果,完成下列列联表.并判断能否在犯错误的概率不超过![]() 的前提下认为科类的选择与性别有关?
的前提下认为科类的选择与性别有关?
选择自然科学类 | 选择社会科学类 | 合计 | |
男生 | |||
女生 | |||
合计 |
附: 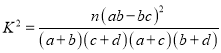 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|1<x<3},集合B={x|2m<x<1-m}.
(1)当m=-1时,求A∪B;
(2)若AB,求实数m的取值范围;
(3)若A∩B=,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为招聘新员工设计了一个面试方案:应聘者从![]() 道备选题中一次性随机抽取
道备选题中一次性随机抽取![]() 道题,按照题目要求独立完成规定:至少正确完成其中
道题,按照题目要求独立完成规定:至少正确完成其中![]() 道题的便可通过.已知
道题的便可通过.已知![]() 道备选题中应聘者甲有
道备选题中应聘者甲有![]() 道题能正确完成,
道题能正确完成,![]() 道题不能完成;应聘者乙每题正确完成的概率都是
道题不能完成;应聘者乙每题正确完成的概率都是![]() ,且每题正确完成与否互不影响
,且每题正确完成与否互不影响
(1)分别求甲、乙两人正确完成面试题数的分布列,并计算其数学期望;
(2)请分析比较甲、乙两人谁的面试通过的可能性大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com