
【题目】把电影院的4张电影票随机地分发给甲、乙、丙、丁4人,每人分得1张,事件“甲分得4排1号”与事件“乙分得4排1号”是( )
A.对立事件B.不可能事件C.互斥但不对立事件D.以上答案都不对
科目:高中数学 来源: 题型:
【题目】从高三学生中抽取![]() 名学生参加数学竞赛,成绩(单位:分)的分组及各数据绘制的频率分布直方图如图所示,已知成绩的范围是区间
名学生参加数学竞赛,成绩(单位:分)的分组及各数据绘制的频率分布直方图如图所示,已知成绩的范围是区间![]() ,且成绩在区间
,且成绩在区间![]() 的学生人数是
的学生人数是![]() 人,
人,

(1)求![]() 的值;
的值;
(2)若从数学成绩(单位:分)在![]() 的学生中随机选取
的学生中随机选取![]() 人进行成绩分析
人进行成绩分析
①列出所有可能的抽取结果;
②设选取的![]() 人中,成绩都在
人中,成绩都在![]() 内为事件
内为事件![]() ,求事件
,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中装有除颜色外其他均相同的编号为a,b的两个黑球和编号为c,d,e的三个红球,从中任意摸出两个球.
(1)求恰好摸出1个黑球和1个红球的概率:
(2)求至少摸出1个黑球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
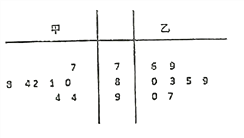
【题目】为了调查观众对电视剧《风筝》的喜爱程度,某电视台举办了一次现场调查活动.在参加此活动的甲、乙两地观众中,各随机抽取了8名观众对该电视剧评分做调查(满分100分),被抽取的观众的评分结果如图所示
(Ⅰ)计算:①甲地被抽取的观众评分的中位数;
②乙地被抽取的观众评分的极差;
(Ⅱ)用频率估计概率,若从乙地的所有观众中再随机抽取4人进行评分调查,记抽取的4人评分不低于90分的人数为![]() ,求
,求![]() 的分布列与期望;
的分布列与期望;
(Ⅲ)从甲、乙两地分别抽取的8名观众中各抽取一人,在已知两人中至少一人评分不低于90分的条件下,求乙地被抽取的观众评分低于90分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com