
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),圆
为参数),圆![]() 的方程为
的方程为![]() .以原点
.以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(Ⅰ)求直线![]() 及圆
及圆![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)若直线![]() 与圆
与圆![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:高中数学 来源: 题型:
【题目】5名男生3名女生参加升旗仪式:
(1)站两横排,3名女生站前排,5名男生站后排有多少种站法?
(2)站两纵列,每列4人,每列都有女生且女生站在男生前面,有多少种排列方法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两个班级均为40人,进行一门考试后,按学生考试成绩及格与不及格进行统计,甲班及格人数为36人,乙班及格人数为24人.
(1)根据以上数据建立一个2×2的列联表;
(2)试判断能否有99.5%的把握认为“考试成绩与班级有关”?参考公式:![]()
![]() ;n=a+b+c+d
;n=a+b+c+d
P( | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() ,
,![]() 分别是其左、右焦点,且过点
分别是其左、右焦点,且过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若在直线![]() 上任取一点
上任取一点![]() ,从点
,从点![]() 向
向![]() 的外接圆引一条切线,切点为
的外接圆引一条切线,切点为![]() .问是否存在点
.问是否存在点![]() ,恒有
,恒有![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是亚太区域国家与地区加强多边经济联系、交流与合作的重要组织,其宗旨和目标是“相互依存、共同利益,坚持开放性多边贸易体制和减少区域间贸易壁垒.”2017年
是亚太区域国家与地区加强多边经济联系、交流与合作的重要组织,其宗旨和目标是“相互依存、共同利益,坚持开放性多边贸易体制和减少区域间贸易壁垒.”2017年![]() 会议于11月10日至11日在越南岘港举行.某研究机构为了了解各年龄层对
会议于11月10日至11日在越南岘港举行.某研究机构为了了解各年龄层对![]() 会议的关注程度,随机选取了100名年龄在
会议的关注程度,随机选取了100名年龄在![]() 内的市民进行了调查,并将结果绘制成如图所示的频率分布直方图(分组区间分别为
内的市民进行了调查,并将结果绘制成如图所示的频率分布直方图(分组区间分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
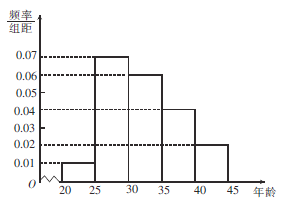
(1)求选取的市民年龄在![]() 内的人数;
内的人数;
(2)若从第3,4组用分层抽样的方法选取5名市民进行座谈,再从中选取2人参与![]() 会议的宣传活动,求参与宣传活动的市民中至少有一人的年龄在
会议的宣传活动,求参与宣传活动的市民中至少有一人的年龄在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知变量![]() 之间的线性回归方程为
之间的线性回归方程为![]() ,且变量
,且变量![]() 之间的一组相关数据如表所示,则下列说法错误的是( )
之间的一组相关数据如表所示,则下列说法错误的是( )
x | 6 | 8 | 10 | 12 |
y | 6 | m | 3 | 2 |
A. 变量![]() 之间呈现负相关关系
之间呈现负相关关系
B. ![]() 的值等于5
的值等于5
C. 变量![]() 之间的相关系数
之间的相关系数![]()
D. 由表格数据知,该回归直线必过点(9,4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省2016年高中数学学业水平测试的原始成绩采用百分制,发布成绩使用等级制.各等制划分标准为:85分及以上,记为![]() 等;分数在
等;分数在![]() 内,记为
内,记为![]() 等;分数在
等;分数在![]() 内,记为
内,记为![]() 等;60分以下,记为
等;60分以下,记为![]() 等.同时认定
等.同时认定![]() 为合格,
为合格, ![]() 为不合格.已知甲,乙两所学校学生的原始成绩均分布在
为不合格.已知甲,乙两所学校学生的原始成绩均分布在![]() 内,为了比较两校学生的成绩,分别抽取50名学生的原始成绩作为样本进行统计,按照
内,为了比较两校学生的成绩,分别抽取50名学生的原始成绩作为样本进行统计,按照![]() 的分组作出甲校的样本频率分布直方图如图1所示,乙校的样本中等级为
的分组作出甲校的样本频率分布直方图如图1所示,乙校的样本中等级为![]() 的所有数据茎叶图如图2所示.
的所有数据茎叶图如图2所示.
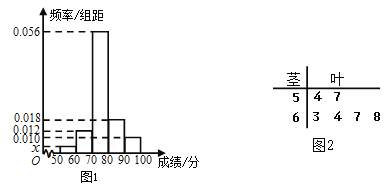
(Ⅰ)求图1中![]() 的值,并根据样本数据比较甲乙两校的合格率;
的值,并根据样本数据比较甲乙两校的合格率;
(Ⅱ)在选取的样本中,从甲,乙两校![]() 等级的学生中随机抽取3名学生进行调研,用
等级的学生中随机抽取3名学生进行调研,用![]() 表示所抽取的3名学生中甲校的学生人数,求随机变量
表示所抽取的3名学生中甲校的学生人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 垂直于
垂直于![]() 所在的平面
所在的平面![]() ,
,![]() 为
为![]() 的直径,
的直径,![]() 是弧
是弧![]() 上的一个动点(不与端点
上的一个动点(不与端点![]() 重合),
重合),![]() 为
为![]() 上一点,且
上一点,且![]() 是线段
是线段![]() 上的一个动点(不与端点
上的一个动点(不与端点![]() 重合).
重合).

(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() 是弧
是弧![]() 的中点,
的中点,![]() 是锐角,且三棱锥
是锐角,且三棱锥![]() 的体积为
的体积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com