
【题目】如图,在正三棱柱ABC-A1B1C1中,AB=3,AA1=4,M为AA1的中点,P是BC上的一点,且由P沿棱柱侧面经过棱CC1到M的最短路线长为![]() ,设这条最短路线与CC1的交点为N.求:
,设这条最短路线与CC1的交点为N.求:

(1)该三棱柱的侧面展开图的对角线的长;
(2)PC和NC的长.
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 的中点.
的中点.
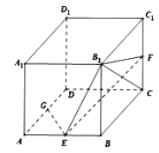
(1)求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(2)棱![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,正确的为________(正确序号全部填上)
(1)空间中,一个角的两边与另一个角的两边分别平行,则这两个角相等或互补;
(2)一个二面角的两个半平面与另一个二面角的两个半平面分别垂直,则这两个二面角相等或互补;
(3)直线![]() ,
,![]() 为异面直线,所成角的大小为
为异面直线,所成角的大小为![]() ,过空间一点
,过空间一点![]() 作直线
作直线![]() ,使l与直线
,使l与直线![]() 及直线
及直线![]() 都成相等的角
都成相等的角![]() ,这样的直线可作3条;
,这样的直线可作3条;
(4)直线![]() 与平面
与平面![]() 相交,过直线
相交,过直线![]() 可作唯一的平面与平面
可作唯一的平面与平面![]() 垂直.
垂直.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地区某种农产品的年产量![]() (单位:吨)对价格
(单位:吨)对价格![]() (单位:千元/吨)和利润
(单位:千元/吨)和利润![]() 的影响,对近五年该农产品的年产量和价格统计如下表:
的影响,对近五年该农产品的年产量和价格统计如下表:
| 1 | 2 | 3 | 4 | 5 |
| 8 | 6 | 5 | 4 | 2 |
已知![]() 和
和![]() 具有线性相关关系.
具有线性相关关系.
(1)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若每吨该农产品的成本为2.2千元,假设该农产品可全部卖出,预测当年产量为多少吨时,年利润![]() 取到最大值?
取到最大值?
参考公式:  .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 同时满足条件:①存在互异的
同时满足条件:①存在互异的![]() 使得
使得![]() (
(![]() 为常数);
为常数);
②当![]() 且
且![]() 时,对任意
时,对任意![]() 都有
都有![]() ,则称数列
,则称数列![]() 为双底数列.
为双底数列.
(1)判断以下数列![]() 是否为双底数列(只需写出结论不必证明);
是否为双底数列(只需写出结论不必证明);
①![]() ; ②
; ②![]() ; ③
; ③![]()
(2)设![]() ,若数列
,若数列![]() 是双底数列,求实数
是双底数列,求实数![]() 的值以及数列
的值以及数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)设![]() ,是否存在整数
,是否存在整数![]() ,使得数列
,使得数列![]() 为双底数列?若存在,求出所有的
为双底数列?若存在,求出所有的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 是两条不同的直线,
是两条不同的直线,![]() ,
,![]() ,
,![]() 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若![]() ,
,![]() ,则
,则![]()
②若![]() ,
,![]() ,
,![]() ,则
,则![]()
③若![]() ,
,![]() ,则
,则![]()
④若![]() ,
,![]() ,则
,则![]()
其中正确命题的序号是( )
A.①和②B.②和③C.③和④D.①和④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年,在《我是演说家》第四季这档节目中,英国华威大学留学生游斯彬的“数学之美”的演讲视频在微信朋友圈不断被转发,他的视角独特,语言幽默,给观众留下了深刻的印象.某机构为了了解观众对该演讲的喜爱程度,随机调查了观看了该演讲的140名观众,得到如下的列联表:(单位:名)
男 | 女 | 总计 | |
喜爱 | 40 | 60 | 100 |
不喜爱 | 20 | 20 | 40 |
总计 | 60 | 80 | 140 |
(1)根据以上列联表,问能否在犯错误的概率不超过0.05的前提下认为观众性别与喜爱该演讲有关.(精确到0.001)
(2)从这60名男观众中按对该演讲是否喜爱采取分层抽样,抽取一个容量为6的样本,然后随机选取两名作跟踪调查,求选到的两名观众都喜爱该演讲的概率.
附:临界值表
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.705 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为1,线段
的棱长为1,线段![]() 上有两个动点
上有两个动点![]() ,且
,且![]() ,现有如下四个结论:
,现有如下四个结论:
![]() ;
;![]() 平面
平面![]() ;
;
![]() 三棱锥
三棱锥![]() 的体积为定值;
的体积为定值;![]() 异面直线
异面直线![]() 所成的角为定值,
所成的角为定值,
其中正确结论的序号是______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足:
满足:![]()
(1) 证明:数列![]() 是等比数列;
是等比数列;
(2) 求使不等式![]() 成立的所有正整数m、n的值;
成立的所有正整数m、n的值;
(3) 如果常数0 < t < 3,对于任意的正整数k,都有![]() 成立,求t的取值范围.
成立,求t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com