
(08年福建卷理)(本小题满分14分)
已知函数![]() .
.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)记![]() 在区间
在区间![]() (n∈N*)上的最小值为
(n∈N*)上的最小值为![]() ,令
,令![]() .
.
① 如果对一切n,不等式![]() 恒成立,求实数c的取值范围;
恒成立,求实数c的取值范围;
() 求证:![]() .
.
解析:解法一:
(I)因为![]() ,所以函数定义域为
,所以函数定义域为![]() ,且
,且![]() 。
。
由![]() 得
得![]() ,
,![]() 的单调递增区间为
的单调递增区间为![]() ;
;
由![]() <0得
<0得![]() ,
,![]() 的单调递增区间为(0,+
的单调递增区间为(0,+![]() ).
).
(Ⅱ)因为![]() 在
在![]() 上是减函数,所以
上是减函数,所以![]() ,
,
则![]() .
.
()![]()
![]()
又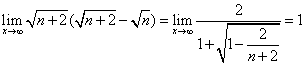 ,
,
因此![]() ,即实数c的取值范围是
,即实数c的取值范围是![]() .
.
() 由①知![]()
因为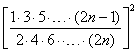
![]()
所以![]() <
<![]()
![]() ,
,
则![]()
![]()
![]() .
.
解法二:
(I)同解法一。
(Ⅱ)因为![]() 在
在![]() 上是减函数,所以
上是减函数,所以![]() ,
,
则![]() .
.
() 因为![]() 对
对![]() 恒成立,
恒成立,
所以![]() 对
对![]() 恒成立。
恒成立。
则![]() 对
对![]() 恒成立。
恒成立。
设![]() ,
,![]() ,则
,则![]() 对
对![]() 恒成立。
恒成立。
考虑![]() 。
。
因为![]()
![]() 在
在![]() 内是减函数;则当
内是减函数;则当![]() 时,
时,![]() 随
随![]() 的增大而减小。
的增大而减小。
又因为![]()
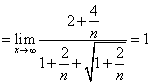 。
。
所以对一切![]() ,
,![]() 。因此
。因此![]() ,即实数c的取值范围是
,即实数c的取值范围是![]() .
.
() 由()知![]()
下面用数学归纳法证明不等式
![]()
![]() ,
,
① 当![]() 时,左边
时,左边![]() ,右边
,右边![]() ,左边
,左边![]() 右边,不等式成立。
右边,不等式成立。
② 假设当![]() 时,不等式成立.即
时,不等式成立.即![]() 。
。
当![]() 时,
时,
![]()
![]()
![]() 。
。
即![]() 时,不等式成立.
时,不等式成立.
综合①、②得,![]()
![]() 成立。
成立。
所以![]()
![]()
![]()
![]() 。
。
![]() .
.
【高考考点】本小题主要考查函数的单调性、最值、不等式、数列等基本知识,考查运用导数研究函数性质的方法,考查分析问题和解决问题的能力,满分14分.
【易错提醒】第一问中导数记不住公式
【备考提示】此题为压轴题,所以平时可以让学生学会放弃一些自己能力范围之外的题目,把多余的时间多花点在中低档题目上,可是80%的分数呀,多么可观,可是纵观历年的高考成绩来看又有多少人真正的做到了这120分?


科目:高中数学 来源: 题型:
(08年福建卷理)(本小题满分12分)
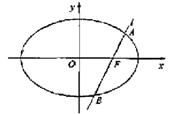
如图,椭圆![]() 的一个焦点是
的一个焦点是![]() ,O为坐标原点.
,O为坐标原点.
(Ⅰ)已知椭圆短轴的两个三等分点与一个焦点构成正三角
形,求椭圆的方程;
(Ⅱ)设过点F的直线l交椭圆于A、B两点.若直线l绕点F
任意转动,恒有![]() ,求a的取值范围.
,求a的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
(08年福建卷理)(本小题满分12分)
如图,椭圆![]() 的一个焦点是
的一个焦点是![]() ,O为坐标原点.
,O为坐标原点.
(Ⅰ)已知椭圆短轴的两个三等分点与一个焦点构成正三角
形,求椭圆的方程;
(Ⅱ)设过点F的直线l交椭圆于A、B两点.若直线l绕点F
任意转动,恒有![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年福建卷理)(本小题满分12分)
某项考试按科目A、科目B依次进行,只有当科目A成绩合格时,才可继续参加科
目B的考试。已知每个科目只允许有一次补考机会,两个科目成绩均合格方可获得证书。现某人参加这项考试,科目A每次考试成绩合格的概率均为![]() ,科目B每次考试成绩合格的概率均为
,科目B每次考试成绩合格的概率均为![]() .假设各次考试成绩合格与否均互不影响.
.假设各次考试成绩合格与否均互不影响.
(Ⅰ)求他不需要补考就可获得证书的概率;
(Ⅱ)在这项考试过程中,假设他不放弃所有的考试机会,记他参加考试的次数为![]() ,求
,求![]() 的数学期望E
的数学期望E![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年福建卷理)(本小题满分12分)
已知函数![]() .
.
(Ⅰ)设![]() 是正数组成的数列,前n项和为
是正数组成的数列,前n项和为![]() ,其中
,其中![]() .若点
.若点![]() (n∈N*)在函数
(n∈N*)在函数![]() 的图象上,求证:点
的图象上,求证:点![]() 也在
也在![]() 的图象上;
的图象上;
(Ⅱ)求函数![]() 在区间
在区间![]() 内的极值.
内的极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年福建卷理)(本小题满分12分)
如图,在四棱锥![]() 中,则面PAD⊥底面
中,则面PAD⊥底面![]() ,侧棱
,侧棱![]() ,底面
,底面![]() 为直角梯形,其中
为直角梯形,其中![]()
![]() ,
,![]() ,O为
,O为![]() 中点。
中点。
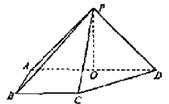
(Ⅰ)求证:PO⊥平面![]() ;
;
(Ⅱ)求异面直线PD与CD所成角的大小;
(Ⅲ)线段AD上是否存在点Q,使得它到平面PCD的距离为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com