
【题目】某快递网点收取快递费用的标准是重量不超过![]() 的包裹收费10元,重量超过
的包裹收费10元,重量超过![]() 的包裹,除收费10元之外,超过
的包裹,除收费10元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 计算)需要再收费5元.该公司近60天每天揽件数量的频率分布直方图如下图所示(同一组数据用该区间的中点值作代表).
计算)需要再收费5元.该公司近60天每天揽件数量的频率分布直方图如下图所示(同一组数据用该区间的中点值作代表).
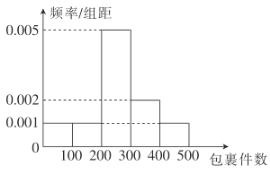
(1)求这60天每天包裹数量的平均数和中位数;
(2)该快递网点负责人从收取的每件快递的费用中抽取5元作为工作人员的工资和网点的利润,剩余的作为其他费用.已知该网点有工作人员3人,每人每天工资100元,以样本估计总体,试估计该网点每天的利润有多少元?
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域为R,如果存在函数g(x),使得f(x)≥g(x)对于一切实数x都成立,那么称g(x)为函数f(x)的一个承托函数.已知函数f(x)=ax2+bx+c的图象经过点(-1,0).
(1)若a=1,b=2.写出函数f(x)的一个承托函数(结论不要求证明);
(2)判断是否存在常数a,b,c,使得y=x为函数f(x)的一个承托函数,且f(x)为函数![]() 的一个承托函数?若存在,求出a,b,c的值;若不存在,说明理由.
的一个承托函数?若存在,求出a,b,c的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)将![]() ,
, ![]() 的方程化为普通方程,并说明它们分别表示什么曲线?
的方程化为普通方程,并说明它们分别表示什么曲线?
(2)以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,已知直线
轴的正半轴为极轴,建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() .若
.若![]() 上的点
上的点![]() 对应的参数为
对应的参数为![]() ,点
,点![]() 在
在![]() 上,点
上,点![]() 为
为![]() 的中点,求点
的中点,求点![]() 到直线
到直线![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有一组圆![]() .下列四个命题正确的是( )
.下列四个命题正确的是( )
A. 存在![]() ,使圆与
,使圆与![]() 轴相切
轴相切
B. 存在一条直线与所有的圆均相交
C. 存在一条直线与所有的圆均不相交
D. 所有的圆均不经过原点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有编号为1,2,3,…,100的100把锁,利用中国剩余定理的原理设置开锁密码,规则为:将锁的编号依次除以3,5,7所得的三个余数作为该锁的开锁密码,这样,每把锁都有一个三位数字的开锁密码.例如,编号为52的锁所对应的开锁密码是123,开锁密码为232所对应的锁的编号是23.若一把锁的开锁密码为203,则这把锁的编号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)分别求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,交曲线
两点,交曲线![]() 于
于![]() ,
,![]() 两点,求
两点,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年1月22日,国新办发布消息:新型冠状病毒来源于武汉一家海鲜市场非法销售的野生动.专家通过全基因组比对发现此病毒与2003年的非典冠状病毒以及此后的中东呼吸综合征冠状病毒,分别达到70%和40%的序列相似性.这种新型冠状病毒对人们的健康生命带来了严重威胁因此,某生物疫苗研究所加紧对新型冠状病毒疫苗进行实验,并将某一型号疫苗用在动物小白鼠身上进行科研和临床实验,得到统计数据如下:
未感染病毒 | 感染病毒 | 总计 | |
未注射疫苗 | 20 |
|
|
注射疫苗 | 30 |
|
|
总计 | 50 | 50 | 100 |
现从所有试验小白鼠中任取一只,取到“注射疫苗”小白鼠的概率为![]() .
.
(1)求![]() 列联表中的数据
列联表中的数据![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)能否有99.9%把握认为注射此种疫苗对预防新型冠状病毒有效?
附:![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 垂直于直角梯形
垂直于直角梯形![]() ,
,![]() ,
,![]() 为
为![]() 中点,
中点,![]() ,
,![]() .
.
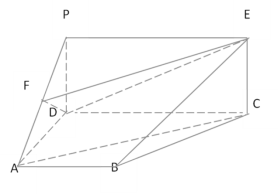
(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() ?若存在,请求出
?若存在,请求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com