
【题目】已知椭圆![]() :
: ![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
, ![]() ,离心率为
,离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,
上, ![]() ,
, ![]() ,过
,过![]() 与坐标轴不垂直的直线
与坐标轴不垂直的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,
两点, ![]() 为
为![]() ,
, ![]() 的中点.
的中点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知点![]() ,且
,且![]() ,求直线
,求直线![]() 所在的直线方程.
所在的直线方程.
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 分别是椭圆
分别是椭圆![]()
![]()
![]() 的左、右焦点,点
的左、右焦点,点![]() 是椭圆
是椭圆![]() 上一点,且
上一点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,若
两点,若![]() ,其中
,其中![]() 为坐标原点,判断
为坐标原点,判断![]() 到直线
到直线![]() 的距离是否为定值?若是,求出该定值;若不是,请说明理由.
的距离是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,双曲线
,双曲线![]() 的一条渐近线与
的一条渐近线与![]() 轴所成的夹角为
轴所成的夹角为![]() ,且双曲线的焦距为
,且双曲线的焦距为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
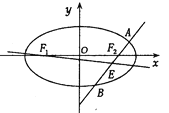
(2)设![]() 分别为椭圆
分别为椭圆![]() 的左,右焦点,过
的左,右焦点,过![]() 作直线
作直线![]() (与
(与![]() 轴不重合)交椭圆于
轴不重合)交椭圆于![]() ,
, ![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(数学文卷·2017届湖北省黄冈市高三上学期期末考试第16题) “中国剩余定理”又称“孙子定理”.1852年英国来华传教伟烈亚利将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年,英国数学家马西森指出此法符合1801年由高斯得出的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”. “中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将2至2017这2016个数中能被3除余1且被5除余1的数按由小到大的顺序排成一列,构成数列![]() ,则此数列的项数为__________.
,则此数列的项数为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】观察图中各正方形图案,每条边上有an个圆点,第an个图案中圆点的个数是an,按此规律推断出所有圆点总和Sn与n的关系式为( )
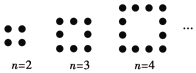
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
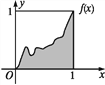
【题目】设函数y=f(x)在区间[0,1]上的图象是连续不断的一条曲线,且恒有0≤f(x)≤1,可以用随机模拟方法近似计算由曲线y=f(x)及直线x=0,x=1,y=0所围成部分的面积S.先产生两组(每组N个)0~1区间上的均匀随机数x1,x2,…,xN和y1,y2,…,yN,由此得到N个点(xi,yi)(i=1,2,…,N).再数出其中满足yi≤f(xi)(i=1,2,…,N)的点数N1,那么由随机模拟方法可得S的近似值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com