
【题目】已知二次函数![]() 在
在![]() 处取得极值,且在
处取得极值,且在![]() 点处的切线与直线
点处的切线与直线![]() 平行.
平行.
(1)求![]() 的解析式;
的解析式;
(2)求函数![]() 的单调递增区间及极值。
的单调递增区间及极值。
(3)求函数![]() 在
在![]() 的最值。
的最值。
【答案】(1)![]() .
.
(2)增区间为![]() ,
,![]() .在
.在![]() 有极小值为0。在
有极小值为0。在![]() 有极大值4/27。
有极大值4/27。
(3)![]() 的最大值为2,最小值为0。
的最大值为2,最小值为0。
【解析】试题分析:(1)第一步,求函数的导数,第二步:根据![]() 处取得极值,知
处取得极值,知![]() ,根据导数的几何意义知;在
,根据导数的几何意义知;在![]() 处的导数等于
处的导数等于![]() ,解得
,解得![]() ,第三步,代入写出
,第三步,代入写出![]() ,令
,令![]() ,得到极值点,最后,解出
,得到极值点,最后,解出![]() ;(2)根据(1)得到的结论,可知
;(2)根据(1)得到的结论,可知![]() 上的单调性,以及极值,比较端点值和极值的大小,就得到最大值和最小值.
上的单调性,以及极值,比较端点值和极值的大小,就得到最大值和最小值.
试题解析:解:(1) 由![]() ,可得
,可得![]() .由题设可得
.由题设可得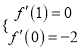
即![]() .解得
.解得![]() ,
, ![]() .所以
.所以![]() .
.
由题意得![]()
所以![]() .
.
令![]() ,得
,得![]() ,
, ![]() .
.
当![]() 变化时,
变化时, ![]() ,
, ![]() 变化情况如下表:
变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
| 单调递增 | 4/27 | 单调递减 | 0 | 单调递增 |
所以函数![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() .
.
(2)因为在![]() 时函数
时函数![]() 有极小值为0.在
有极小值为0.在![]() 时函数
时函数![]() 有极大值
有极大值![]() .
.
又![]() ,
,
所以函数![]() 的最大值为2,最小值为0.
的最大值为2,最小值为0.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 分别是椭圆
分别是椭圆![]()
![]()
![]() 的左、右焦点,点
的左、右焦点,点![]() 是椭圆
是椭圆![]() 上一点,且
上一点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,若
两点,若![]() ,其中
,其中![]() 为坐标原点,判断
为坐标原点,判断![]() 到直线
到直线![]() 的距离是否为定值?若是,求出该定值;若不是,请说明理由.
的距离是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取一个年份,对西安市该年4月份的天气情况进行统计,结果如下:
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
天气 | 晴 | 雨 | 阴 | 阴 | 阴 | 雨 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 晴 |
日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
天气 | 晴 | 阴 | 雨 | 阴 | 阴 | 晴 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 雨 |
(1)在4月份任取一天,估计西安市在该天不下雨的概率;
(2)西安市某学校拟从4月份的一个晴天开始举行连续2天的运动会,估计运动会期间不下雨的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直.(注:
垂直.(注: ![]() 为自然对数的底数)
为自然对数的底数)
(1)求![]() 的值;
的值;
(2)若函数![]() 在区间
在区间![]() 上存在极值,求实数
上存在极值,求实数![]() 的取值范围;
的取值范围;
(3)求证:当![]() 时,
时, ![]() 恒成立.
恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,且点
,且点![]() 在椭圆
在椭圆![]() 上.
上.
⑴求椭圆![]() 的标准方程;
的标准方程;
⑵已知动直线![]() 过点
过点![]() 且与椭圆
且与椭圆![]() 交于
交于![]() 两点.试问
两点.试问![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com