A
分析:题目给出了一个抽象函数y=f(x)满足的两个条件,条件(1)说明了函数的奇偶性,条件(2)给出了函数的周期,结合以上两个性质,即可得到函数图象的大致形状.
解答:定义在R上的函数y=f(x)满足f(x)+f(-x)=0,即f(-x)=-f(x),
所以函数y=f(x)是定义在实数上的奇函数,
又满足f(x+2)=f(x),所以,函数是定义域内以2为周期的周期函数,
结合以上两点可知,给出的函数f(x)是定义在实数集上以2为周期的奇函数.
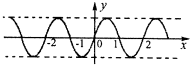
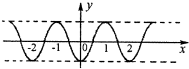
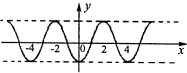
由选项中的四个图象看出,只有选项A中的图象符合.
故选A.
点评:本题考查了函数图象的周期性,考查了奇偶函数图象的对称性,函数的图象关于原点中心对称是函数为奇函数的充要条件,关于y轴轴对称是函数为偶函数的充要条件.此题是基础题.

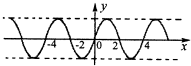


 名校课堂系列答案
名校课堂系列答案